In the world of data science and machine learning, creating a predictive model is only half the battle. How do you know if your model is actually any good? Measuring its accuracy is a critical step, and one of the most fundamental tools for this task is the mean squared error (MSE). Understanding how to calculate and interpret this metric is essential for anyone looking to build reliable and effective models.
Ready to master model evaluation? Dive into our comprehensive guide on statistical analysis techniques and take your skills to the next level.
What Exactly is Mean Squared Error?

At its core, the mean squared error provides a way to quantify the difference between the values a model predicts and the actual, observed values. In simpler terms, it measures the average “error” of your model’s predictions. The calculation involves a few straightforward steps:
- Calculate the Error: For each data point, subtract the predicted value from the actual value. This difference is called the residual or error.
- Square the Error: Square each of these error values. This crucial step serves two purposes. First, it ensures all error values are non-negative (squaring a negative number results in a positive one). Second, it penalizes larger errors more heavily than smaller ones. A model that is off by 10 will be penalized more significantly than a model that is off by 2.
- Find the Average: Sum up all the squared errors and divide by the total number of data points.
This process gives you a single value, the mean squared error, which encapsulates the overall performance of your model. A lower MSE indicates that the model’s predictions are, on average, closer to the actual values, signifying a better fit.
A More Intuitive Metric: Root Mean Squared Error

While MSE is incredibly useful for training and comparing models (its mathematical properties make it ideal for optimization algorithms), it has one drawback: its units are squared. For example, if you are predicting house prices in dollars, the MSE will be in “dollars squared,” which isn’t very intuitive.
This is where the root mean squared error (RMSE) comes in. As the name suggests, RMSE is simply the square root of the MSE. By taking the square root, we convert the error metric back into the original units of the target variable. This makes the RMSE much easier to interpret. An RMSE of $50,000 in our house price prediction model means that, on average, the model’s predictions are off by about $50,000. This direct interpretability makes RMSE a popular choice for reporting a model’s performance in a real-world context.
A Different Perspective on Fit: The R-Squared Formula
While MSE and RMSE tell you about the magnitude of the prediction error, they don’t tell the whole story. Another vital metric is R-squared (R²), also known as the coefficient of determination. Instead of focusing on the error, R-squared measures the proportion of the variance in the dependent variable that is predictable from the independent variable(s).
The r squared formula essentially compares your model’s performance to a simple baseline model that just predicts the mean of the target variable for all observations. An R-squared value ranges from 0 to 1 (or 0% to 100%) and tells you how much of the “scatter” in the actual data is explained by your model.
- An R² of 0 means your model is no better than the baseline mean model.
- An R² of 1 means your model perfectly explains the variability in the data.
MSE vs. R-Squared: Which One to Use?
The choice between these metrics depends on your goal. MSE and RMSE are absolute measures of fit—they give you an error value in specific units. They are excellent for comparing different models built on the same dataset. If Model A has a lower RMSE than Model B, it is generally the better-performing model.
R-squared, on the other hand, is a relative measure of fit. It provides context about your model’s explanatory power. A high R-squared is often desirable, but it doesn’t automatically mean your model is unbiased or that the predictions are accurate in an absolute sense. A good practice is to use them together. Use MSE/RMSE to understand the prediction error’s magnitude and R-squared to understand the model’s explanatory power.
Important Key Concepts Related to Mean Squared Error
1. Error / Residual
The difference between predicted value y^ and actual value y.
e=y−y^
2. Squared Error
Each residual is squared to penalize large errors more heavily.
3. Mean of Squared Errors
The average of all squared errors forms the Mean Squared Error (MSE).
4. Loss Function
MSE is one of the most commonly used loss functions for regression models.
5. Convexity
MSE is a convex function—meaning optimization algorithms like Gradient Descent can easily minimize it.
6. Sensitivity to Outliers
Because errors are squared, a single extreme outlier can disproportionately affect the MSE value.
Examples of MSE (Simple & Practical)
Example 1: Small Dataset
Actual Values (y): 5, 7, 8
Predicted Values (ŷ): 6, 6, 10
Errors = -1, 1, -2
Squared Errors = 1, 1, 4
MSE=1+1+4 / 3=2
Example 2: Machine Learning Prediction Example
Suppose a model predicts monthly sales:
| Month | Actual Sales | Predicted Sales |
| Jan | 1200 | 1100 |
| Feb | 1500 | 1600 |
| Mar | 1000 | 900 |
MSE represents how far predictions deviate from actual sales in squared units.
Practical Applications of MSE
- Regression Model Evaluation
- Performance metric in machine learning competitions (Kaggle)
- Forecasting models like ARIMA, Prophet, LSTM
- Signal processing & image compression
- Financial modeling—risk estimation
- Recommendation systems
- Manufacturing—predictive maintenance errors
- Healthcare—predictive diagnostics
Why Is MSE Important in Machine Learning?
Universal Loss Function
MSE is widely used for training linear regression, neural networks, and many supervised learning algorithms.
Penalizes Large Errors
This ensures models try hard to avoid big mistakes.
Smooth & Differentiable
Essential for gradient-based optimization.
Easy to Compute
Simple mathematical formulation that scales well.
How Is MSE Calculated? (Formula + Breakdown)
Formula
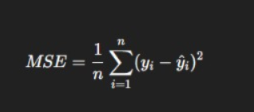
Where:
- yi = Actual values
- y^i = Predicted values
- n = Number of samples
Step-by-Step:
- Subtract predicted from actual
- Square the difference
- Sum all squared errors
- Divide by total observations
Interpreting MSE Results
Lower MSE = Better Model
Smaller errors mean predictions are closer to the actual values.
Higher MSE = Poor Performance
The model is making large or inconsistent errors.
Units Are Squared
This makes MSE less interpretable compared to RMSE.
Compare Only on Same Dataset
MSE values from different datasets are not comparable.
Comparing Models Using MSE Scores
Use MSE to evaluate:
- Linear Regression vs. Random Forest
- ARIMA vs. Prophet forecasting
- Neural Network vs. Gradient Boosting
Example:
Model A MSE = 120
Model B MSE = 80
➡ Model B performs better for that dataset.
Use cases:
- Feature engineering impact measurement
- Selecting best hyperparameters
- K-fold cross-validation
MSE in Optimization Algorithms Like Gradient Descent
MSE is used as the cost function:
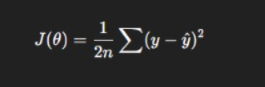
The gradient is:
∂J / ∂θ
Used in:
- Training neural networks
- Linear regression parameter updates
- Polynomial regression
- Deep learning architectures
Why MSE Works Well With Gradient Descent:
- Convex landscape
- Continuous and differentiable
- Guarantees global minimum in linear regression
Pro Tips for Using MSE Effectively
1. Always check for outliers first
Outliers can drastically increase MSE.
2. Use cross-validation instead of single test scores
More reliable evaluation.
3. Prefer RMSE when communicating insights
RMSE is more intuitive.
4. Use MAE alongside MSE
MAE (Mean Absolute Error) is more robust to outliers.
5. Normalize/standardize features for complex models
Improves stability of error metrics.
Roles Requiring Strong Mean Squared Error Skills
Professionals who frequently use MSE include:
- Data Scientists
- Machine Learning Engineers
- AI Researchers
- Business Analysts
- Financial Data Analysts
- Econometricians
- Data Engineers
- Forecasting Specialists
- Signal Processing Engineers
They use MSE to validate predictions, optimize models, and evaluate algorithm performance.
Advantages and Limitations of Using MSE
Advantages
- Easy to compute
- Differentiable (ideal for optimization)
- Penalizes large errors strongly
- Works well with Gaussian noise
- Standard choice in regression tasks
Limitations
- Sensitive to outliers
- Not intuitive (squared units)
- Not suitable for classification models
- Assumes symmetric errors
Use Cases of MSE (Industry-Wise)
1. Finance
- Predicting stock prices
- Credit risk modeling
- Portfolio optimization
2. Healthcare
- Predicting patient readmission
- Disease progression models
3. Retail & E-commerce
- Demand forecasting
- Dynamic pricing models
4. Real Estate
- House price prediction
- Property valuation models
5. Manufacturing
- Predictive maintenance
- Quality control anomaly detection
6. Marketing & CRM
- Customer lifetime value (CLV) prediction
- Churn forecasting
Conclusion: A Holistic View of Model Performance
Ultimately, no single metric can tell you everything about your model’s performance. The mean squared error is a cornerstone of model evaluation, providing a robust way to quantify prediction errors. The root mean squared error builds on this by offering a more intuitive, interpretable value. When combined with insights from the r squared formula, you can gain a comprehensive understanding of your model’s strengths and weaknesses, leading to better decisions and more accurate predictions.
Want to apply these concepts to your own data? Contact our data science experts today for a personalized consultation!
FAQ’s
How to calculate accuracy from mean squared error?
Accuracy isn’t directly calculated from Mean Squared Error (MSE), but a lower MSE indicates a more accurate regression model. You can derive Root Mean Squared Error (RMSE) to interpret error in the same units as the target variable.
What is the mean squared error of a model?
Mean Squared Error (MSE) is a metric that measures how far a model’s predictions are from the actual values by averaging the squared differences between them. Lower MSE means higher prediction accuracy.
Which is better MAE or MSE?
MAE vs MSE depends on your goal:
MAE (Mean Absolute Error) is better when you want a simple, more interpretable metric that treats all errors equally.
MSE (Mean Squared Error) is better when you want to penalize larger errors more heavily, making it useful for models where big mistakes are costly.
In short, use MAE for robustness and MSE for sensitivity to large errors.
What is the top 5 accuracy formula?
Top-5 accuracy measures how often the correct label appears in a model’s top 5 predicted probabilities.
Formula:
Top-5 Accuracy = Number of samples where true label is in top 5 predictions / Total number of samples
What is a good MSE for model?
A “good” MSE depends on the scale of your target variable — there is no universal value.
Generally, lower MSE is better, and an MSE close to 0 indicates highly accurate predictions.



