Bayesian vs Frequentist Statistics: The Ultimate Power Guide to Statistical Thinking

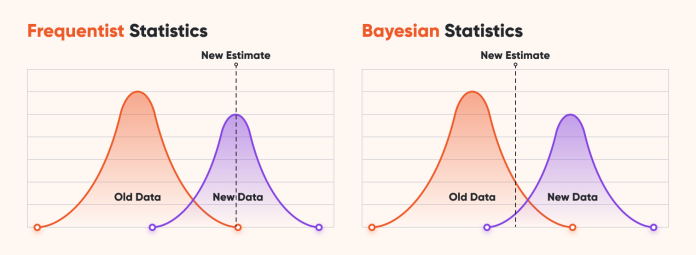
Statistics is the backbone of data science, research, and decision-making. However, one of the most debated topics in the field is Bayesian vs Frequentist Statistics. These two approaches represent fundamentally different philosophies of probability and inference.

• Frequentist statistics relies on long-run frequencies and repeated experiments.
  
• Bayesian statistics incorporates prior knowledge along with observed data to update beliefs.

In this blog, we will explore both methods, highlight their strengths, weaknesses, applications, and practical differences, and help you decide which approach to use in real-world projects.

What is Frequentist Statistics?

Definition and Core Idea

Frequentist statistics is the traditional school of thought where probability is defined as the long-run frequency of an event. In this approach, parameters are considered fixed but unknown constants.

Frequentist Probability Explained

• Probability = Number of favorable outcomes ÷ Total number of trials (in the long run).
  
• Example: The probability of rolling a 6 on a fair die is always 1/6, regardless of prior beliefs.

Real-World Example

Suppose you are conducting A/B testing for a new website feature.

• A Frequentist will run the test multiple times, compute p-values, and decide whether to reject the null hypothesis.
  
• No prior belief about which version is better is considered—only the observed data drives the conclusion.

What is Bayesian Statistics?

Definition and Core Idea

Bayesian statistics defines probability as a degree of belief or plausibility. Parameters are treated as random variables with distributions that can change when new data is observed.

Bayesian Probability Explained

The foundation is Bayes’ Theorem:

P(θ∣Data)=P(Data∣θ)⋅P(θ)​ / P(Data)

Where:

• P(θ): Prior probability (belief before seeing data).
  
• P(Data∣θ): Likelihood of observing the data given parameters.
  
• P(θ∣Data): Posterior probability (updated belief after seeing data).

Real-World Example

Suppose a doctor is diagnosing a disease.

• Prior: 1% of the population has the disease.
  
• New Data: A test shows positive results.
  
• Bayesian Update: Combining prior probability with the test’s accuracy gives the posterior probability that the patient truly has the disease.

Bayesian vs Frequentist Statistics: Key Differences

Aspect	Frequentist Approach	Bayesian Approach
Probability Definition	Long-run frequency	Degree of belief
Parameters	Fixed constants	Random variables
Prior Knowledge	Ignored	Incorporated
Inference	Confidence intervals, p-values	Posterior distributions
Updating Beliefs	Not possible	Possible with Bayes’ theorem

Bayesian vs Frequentist in Machine Learning

Machine learning models often rely on probability for predictions.

• Frequentist ML: Maximum likelihood estimation (MLE), logistic regression, and support vector machines use the frequentist perspective.
  
• Bayesian ML: Bayesian networks, Bayesian optimization, and probabilistic programming use priors and posterior inference to update predictions as new data arrives.

Example:

• In hyperparameter tuning, Bayesian optimization is often more efficient than frequentist grid search because it uses prior knowledge of past iterations.

Advantages of Frequentist Statistics

• Simpler computations (no priors required).
  
• Widely taught and accepted in academia.
  
• Good for large datasets where long-run frequencies are valid.
  
• Established frameworks like p-values and confidence intervals are standardized.

Advantages of Bayesian Statistics

• Allows inclusion of prior knowledge.
  
• Flexible and intuitive for small datasets.
  
• Produces credible intervals that are easier to interpret than confidence intervals.
  
• Useful in real-time decision-making, like fraud detection or medical diagnosis.

Limitations of Frequentist Statistics

• Ignores prior knowledge.
  
• Interpretation of p-values and confidence intervals is often misunderstood.
  
• Not ideal for small sample sizes.
  
• Cannot easily update beliefs with new data.

Limitations of Bayesian Statistics

• Requires choosing priors, which can be subjective.
  
• Computationally expensive, especially with complex models.
  
• Less commonly used in traditional industries compared to frequentist methods.

Bayesian vs Frequentist: Real-Time Use Cases

Medical Decision Making

• Frequentist: A drug is declared effective if the p-value < 0.05.
  
• Bayesian: The doctor updates prior knowledge (e.g., earlier studies) with new clinical trial results to calculate the probability the drug is effective.

A/B Testing in Marketing

• Frequentist: Needs large sample size and fixed-duration experiments.
  
• Bayesian: Allows continuous monitoring and decision-making with smaller datasets.

Predictive Modeling

• Frequentist: Logistic regression using MLE.
  
• Bayesian: Probabilistic models with prior knowledge incorporated.

Natural Language Processing

Bayesian models are often used in topic modeling (e.g., Latent Dirichlet Allocation), while frequentist approaches dominate word embeddings.

Practical Implementation with Python

Example: Bayesian Updating

import pymc3 as pm

import numpy as np

# Data: 6 heads out of 10 coin flips

observed_heads = 6

n_flips = 10

with pm.Model():

    p = pm.Beta("p", alpha=1, beta=1)  # Prior (uniform)

    likelihood = pm.Binomial("likelihood", n=n_flips, p=p, observed=observed_heads)

    trace = pm.sample(2000)

pm.summary(trace)

Frequentist Binomial Estimation

from scipy.stats import binom

n = 10

p = 0.5

prob = binom.pmf(6, n, p)

print("Probability of 6 heads in 10 flips:", prob)

Visual Examples & Diagrams

• Graph comparing confidence interval vs credible interval.
  
• Flowchart of Bayesian updating process.
  
• Diagram showing frequentist vs Bayesian A/B test results.

Choosing the Right Approach

• Use Frequentist methods when you have large datasets, want objectivity, and rely on standard tools like p-values.
  
• Use Bayesian methods when prior knowledge is important, datasets are small, or you need real-time updates.

Historical Debate and Philosophy

The philosophical battle between Bayesian and Frequentist statistics has lasted for centuries.

• Frequentists argue that probability should only describe repeatable experiments. They emphasize objectivity—results should not depend on subjective beliefs.
  
• Bayesians, however, embrace the idea that knowledge is inherently uncertain, and updating beliefs with new evidence is the most natural way to handle uncertainty.

In fact, Pierre-Simon Laplace in the 18th century extensively used Bayesian reasoning for astronomical predictions, while Ronald Fisher and Jerzy Neyman in the 20th century formalized the frequentist hypothesis testing framework.

This historical context matters because it shaped how different scientific fields adopted one philosophy over the other. For decades, medicine, psychology, and biology leaned heavily on Frequentist hypothesis testing, while AI and robotics have accelerated the use of Bayesian reasoning.

Advanced Technical Differences

1. Confidence Interval vs. Credible Interval

• Frequentist Confidence Interval:
  A 95% CI means that if we repeated the experiment infinitely, 95% of the intervals would contain the true parameter. It does not mean there’s a 95% probability the parameter lies in that specific interval.
  
• Bayesian Credible Interval:
  A 95% credible interval directly means there’s a 95% chance the true parameter lies in the given range, based on prior and observed data.

This subtle difference makes Bayesian intervals much easier to interpret for decision-makers.

2. Model Comparison

• Frequentist approaches rely on likelihood ratio tests, AIC (Akaike Information Criterion), or BIC (Bayesian Information Criterion).
  
• Bayesian approaches compare models using Bayes Factors, which quantify the evidence provided by the data in favor of one model over another.

3. Error Control

• Frequentists aim to control Type I (false positive) and Type II (false negative) error rates.
  
• Bayesians instead provide probabilistic statements about hypotheses, avoiding the rigidity of fixed error rates.

Bayesian vs Frequentist in Modern AI

1. Deep Learning Uncertainty
   
   • Frequentist deep learning models provide point estimates and lack natural uncertainty quantification.
     
   • Bayesian deep learning introduces Bayesian neural networks that place distributions over weights, producing not only predictions but also confidence estimates.
     
2. Example: In autonomous driving, Bayesian networks can inform a car whether it’s uncertain about recognizing an obstacle, allowing safer decisions.
   
3. Reinforcement Learning
   
   • Frequentist RL often relies on long-term averages and maximum likelihood estimations.
     
   • Bayesian RL incorporates priors about the environment, helping agents explore efficiently and adapt faster to changing conditions.
     
4. NLP and Generative AI
   
   • Topic modeling (LDA) is Bayesian by design.
     
   • Frequentist approaches dominate in word embeddings and transformer models. However, Bayesian priors can help in few-shot learning where data is scarce.

Advanced Real-Time Applications

1. Fraud Detection in Finance

• Frequentist: Detects anomalies based on thresholds and hypothesis tests.
  
• Bayesian: Updates fraud probability dynamically as new transactions are observed, making it adaptive to changing fraud patterns.

2. Climate Modeling

• Frequentist: Provides fixed confidence intervals for temperature predictions.
  
• Bayesian: Incorporates prior climate data, expert knowledge, and satellite measurements to continuously refine forecasts.

3. Drug Development

• Frequentist trials often require large sample sizes and fixed stopping rules.
  
• Bayesian trials allow adaptive designs where data is analyzed continuously, enabling faster approvals for effective drugs.

Computational Advances

Historically, Bayesian statistics was limited by computational complexity. But now, thanks to Monte Carlo methods and variational inference, Bayesian methods are practical at scale.

• Markov Chain Monte Carlo (MCMC): Allows sampling from complex posterior distributions.
  
• Hamiltonian Monte Carlo (HMC): Efficiently explores high-dimensional spaces (used in PyMC and Stan).
  
• Variational Inference: Scales Bayesian models to massive datasets by approximating posteriors.

In contrast, frequentist methods remain computationally lighter, which makes them more suitable when speed matters and priors are not crucial.

Criticisms and Misconceptions

• Criticism of Frequentist: Over-reliance on p-values often leads to misinterpretation and “p-hacking.” A result with p<0.05 is often treated as a discovery, even if practically insignificant.
  
• Criticism of Bayesian: Priors are subjective. However, modern practice uses non-informative priors or empirical priors derived from historical datasets to reduce bias.

Case Study: A/B Testing

Imagine testing a new pricing strategy for an e-commerce website.

• Frequentist Approach:
  Run the experiment until a predetermined sample size is reached. Use hypothesis testing to accept or reject the new price point.
  
• Bayesian Approach:
  Continuously update the probability that the new strategy improves revenue. Decisions can be made earlier with smaller datasets if the posterior strongly favors one option.

This flexibility explains why many companies (Google, Netflix, Amazon) increasingly rely on Bayesian A/B testing.

The Future of Bayesian vs Frequentist

1. Hybrid Approaches:
   Many modern methods combine both philosophies. For example, empirical Bayes uses data to estimate priors, blending frequentist estimation with Bayesian updating.
   
2. Explainable AI:
   Bayesian methods are gaining traction because their probabilistic nature provides interpretable results, unlike black-box frequentist deep learning.
   
3. Big Data and Cloud Computing:
   Cloud platforms and GPU acceleration have removed many of the computational barriers for Bayesian methods, making them viable in large-scale applications like genomics and personalized medicine.

Conclusion

The debate of Bayesian vs Frequentist Statistics is not about which is “better,” but about which is more appropriate in context. Both approaches are essential for data science, machine learning, and research.

The modern trend in AI and analytics shows a growing adoption of Bayesian approaches, especially with computational advancements. However, frequentist methods remain the backbone of traditional statistics and are widely used in industries.

FAQ’s