A Complete Visual Guide to Domain and Range of a Graph for Concept Mastery

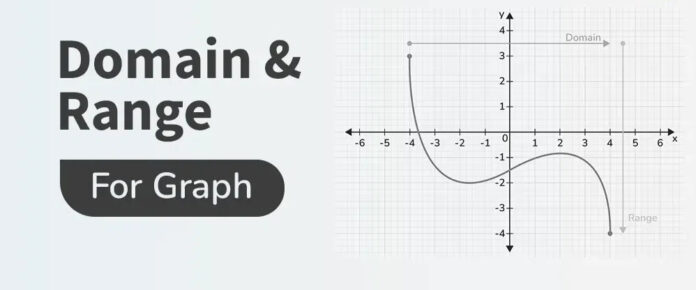
Introduction: Why Graph Understanding Truly Matters

Graphs are one of the most powerful tools humans have developed to understand relationships. From predicting weather patterns to analyzing business profits, graphs convert abstract numbers into meaningful visuals.

Before diving deeper into advanced mathematics, statistics, machine learning, or analytics, learners must master a fundamental concept: understanding how values flow within a graph. This is where the idea of domain and range of a graph becomes essential.

Rather than memorizing formulas, this guide focuses on clarity, visualization, and practical understanding using real-life situations and modern applications.

What Is a Graph in Mathematics?

A graph is a visual representation of the relationship between two variables:

• The horizontal axis (x-axis) shows input values
• The vertical axis (y-axis) shows output values

Each point on the graph represents an ordered pair (x, y).

Graphs help us:

• Identify trends
• Predict outcomes
• Compare quantities
• Analyze behavior over time

Conceptual Meaning of Domain

The domain represents all possible input values for which a function or graph is defined.

In simpler terms:

• Domain answers the question: “What values can x take?”

Key Points About Domain

• Domain values lie on the x-axis
• They represent allowed inputs
• Invalid inputs are excluded

Example:
If a machine only works for temperatures above zero, then negative values are excluded from the domain.

Conceptual Meaning of Range

The range represents all possible output values produced by the function.

Simply put:

• Range answers: “What values can y take?”

Key Points About Range

• Range values lie on the y-axis
• They depend entirely on the domain
• Outputs may be limited or infinite

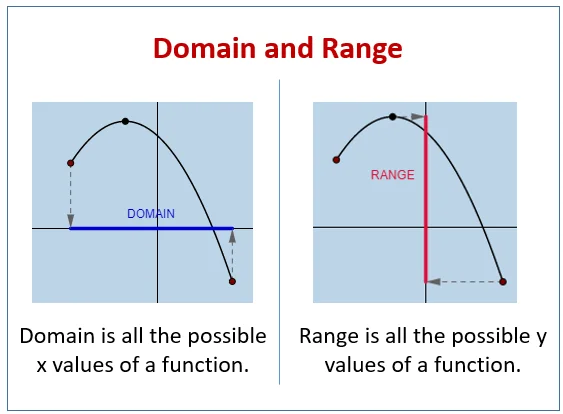
Domain and Range of a Graph Explained Visually

Understanding the domain and range of a graph becomes much easier when viewed visually.

Image Placeholder

Image: Cartesian graph with shaded x-axis and y-axis

Alt text: domain and range of a graph visual explanation

From the image:

• Horizontal spread → Domain
• Vertical spread → Range

Why Domain and Range Are So Important

Understanding domain and range helps in:

• Preventing invalid calculations
• Modeling real-world systems accurately
• Building machine learning models
• Data preprocessing in analytics
• Interpreting scientific experiments

Without defining domain and range, mathematical models become unrealistic or misleading.

Types of Graphs and Their Domain and Range

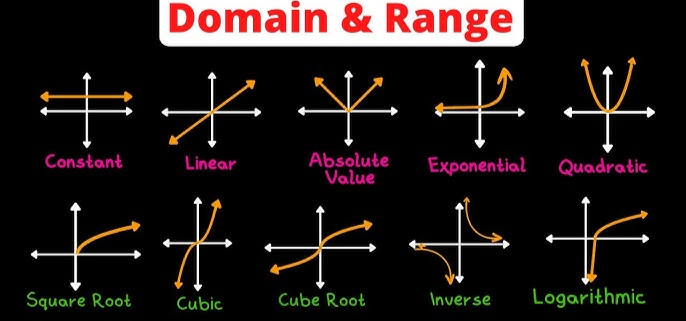
Linear Graphs

• Domain: All real numbers
• Range: All real numbers

Quadratic Graphs

• Domain: All real numbers
• Range: Limited depending on vertex

Square Root Graphs

• Domain: Values ≥ zero
• Range: Values ≥ zero

Rational Graphs

• Domain: Excludes values causing division by zero

Each graph behaves differently, making domain and range of a graph highly context-dependent.

Real-World Examples of Domain and Range

Example 1: Online Shopping Price Filter

• Domain: Prices user can select
• Range: Products displayed

Example 2: Speed vs Fuel Efficiency

• Domain: Speed of vehicle
• Range: Mileage obtained

Example 3: Age vs Height

• Domain: Age values
• Range: Height values

These examples show how domain defines constraints while range shows outcomes.

How to Find Domain of a Graph Step by Step

1. Look at the x-axis coverage
2. Identify gaps or breaks
3. Check for restrictions:
   • Division by zero
   • Square roots of negative numbers
4. Write domain using:
   • Interval notation
   • Set notation

How to Find Range of a Graph Step by Step

1. Observe y-axis values
2. Identify minimum and maximum outputs
3. Look for asymptotes
4. Express range appropriately

Domain and Range Using Tables

x (Domain)	y (Range)
-2	4
-1	1
0	0
1	1
2	4

From the table:

• Domain = {-2, -1, 0, 1, 2}
• Range = {0, 1, 4}

Domain and Range Using Set Notation

• Domain: {x | x ≥ 0}
• Range: {y | y ≤ 10}

Set notation is commonly used in higher mathematics and computer science.

Domain and Range in Functions vs Relations

Functions

• Each input has exactly one output
• Clear domain and range

Relations

• Inputs may have multiple outputs
• Domain may repeat values

Understanding this difference is critical in advanced graph analysis.

Interpretation of Domain and Range in Different Coordinate Systems

While most learners understand graphs in a standard Cartesian plane, domain and range concepts also apply to other coordinate systems.

Polar Coordinates

• Domain represents angle values (θ)
  
• Range represents radius values (r)
  

Example:

• Domain: 0 ≤ θ ≤ 2π
  
• Range: r ≥ 0
  

This is widely used in physics, signal processing, and robotics.

Domain and Range in Piecewise Functions

Piecewise functions define different rules for different input values.

Why This Matters

• Domain is split into intervals
  
• Range varies for each piece
  

Example scenario:

• Electricity billing slabs
  
• Tax calculation models
  

Each slab has a separate domain and produces a different range.

Domain and Range in Exponential and Logarithmic Graphs

Exponential Graphs

• Domain: All real numbers
  
• Range: Positive real numbers
  

Real-life usage:

• Population growth
  
• Compound interest
  
• Viral content spread
  

Logarithmic Graphs

• Domain: Positive real numbers
  
• Range: All real numbers
  

Used in:

• Earthquake intensity (Richter scale)
  
• Sound intensity (decibel scale)
  

Impact of Asymptotes on Domain and Range

Asymptotes influence graph behavior without being part of the graph.

Vertical Asymptotes

• Exclude specific x-values from domain
  

Horizontal Asymptotes

• Restrict the range
  

This is common in:

• Rational functions
  
• Engineering models
  
• Physics simulations
  

Domain and Range in Statistical Graphs

Statistical graphs also follow domain-range logic.

Histogram

• Domain: Class intervals
  
• Range: Frequency
  

Box Plot

• Domain: Data distribution
  
• Range: Quartile values
  

Understanding this helps in:

• Exploratory Data Analysis
  
• Outlier detection
  
• Distribution interpretation
  

Domain and Range in Time-Based Graphs

Time-series data is a major real-world application.

Examples

• Stock price vs time
  
• Website traffic vs date
  
• Heart rate vs time
  

Here:

• Domain = time interval
  
• Range = measured quantity
  

This is crucial in finance, healthcare, and IoT analytics.

Domain and Range Constraints in Real-World Modeling

Mathematical models must respect real-world limitations.

Practical Constraints

• Negative age is invalid
  
• Speed cannot exceed mechanical limits
  
• Revenue cannot be negative
  

Ignoring domain constraints leads to:

• Incorrect predictions
  
• Model failure
  
• Business losses
  

Domain and Range in Programming and Validation Logic

In software systems:

• Domain defines valid input values
  
• Range defines expected output values
  

Example

• API input validation
  
• Form field restrictions
  
• Sensor data limits
  

This ensures system reliability and error prevention.

Relationship Between Domain, Range, and Inverse Functions

For inverse functions:

• Domain of original function becomes range of inverse
  
• Range of original becomes domain of inverse
  

This concept is widely used in:

• Cryptography
  
• Signal decoding
  
• Mathematical transformations
  

Domain and Range in Machine Learning Pipelines

Before training models:

• Input features must lie within expected domain
  
• Output predictions must fall within acceptable range
  

Example

• Image pixel values (0–255)
  
• Probability outputs (0–1)
  

Feature scaling and normalization depend heavily on domain awareness.

Domain and Range Through Graph Transformations

Graph transformations change the appearance of a graph, but they also influence domain and range.

Horizontal Shifts

• Domain shifts left or right
  
• Range remains unchanged
  

Vertical Shifts

• Range shifts up or down
  
• Domain remains unchanged
  

Stretching and Compressing

• Vertical scaling affects range
  
• Horizontal scaling affects domain
  

Real-world use case:
Signal amplification systems rely on scaling transformations that directly affect output range.

Effect of Absolute Value Functions on Domain and Range

Absolute value functions reflect parts of a graph.

Key Observations

• Domain often remains all real numbers
  
• Range becomes non-negative
  

Example:
Temperature deviation models where only magnitude matters, not direction.

Domain and Range in Inequality Graphs

Graphs of inequalities introduce shaded regions.

Domain

All x-values where the inequality holds true

Range

All y-values covered by the shaded region

This is widely used in:

• Optimization problems
  
• Linear programming
  
• Resource allocation models

Domain and Range in Discrete vs Continuous Graphs

Discrete Graphs

• Domain consists of separate values
  
• Range contains individual outputs
  

Examples:

• Number of students vs class sections
  
• Daily sales count
  

Continuous Graphs

• Domain is an interval
  
• Range is also an interval
  

Examples:

• Speed vs time
  
• Temperature changes
  

Domain and Range in Engineering Applications

Electrical Engineering

• Domain: Input voltage
  
• Range: Output current
  

Civil Engineering

• Domain: Load applied
  
• Range: Structural displacement
  

Design safety heavily depends on respecting domain constraints.

Economic Interpretation of Domain and Range

In economics:

• Domain often represents time, price, or quantity
  
• Range represents profit, demand, or cost
  

Example:
Demand curve analysis strictly limits domain to positive price values.

Domain and Range in Scientific Experiments

Experiments require controlled inputs.

• Domain defines experimental conditions
  
• Range defines observed outcomes
  

Ignoring domain boundaries invalidates scientific results.

Domain and Range in Probability Distributions

Continuous Distributions

• Domain: Possible values of random variable
  
• Range: Probability density values
  

Discrete Distributions

• Domain: Countable outcomes
  
• Range: Probability mass values
  

Understanding this is essential in statistics and data modeling.

Domain and Range in Optimization Problems

Optimization problems depend on feasible regions.

• Domain defines constraints
  
• Range defines objective outcomes
  

Applications:

• Cost minimization
  
• Profit maximization
  
• Resource efficiency
  

Domain and Range in Graphical Simulations

Simulation tools rely on bounded inputs.

Example:
Physics engines define:

• Domain for force input
  
• Range for motion output
  

This ensures realistic behavior.

Cognitive Learning Perspective on Domain and Range

Educational research shows:

• Visual representation improves comprehension
  
• Interactive graphs increase retention
  
• Stepwise domain-range identification builds confidence
  

This supports blended learning strategies.

Domain and Range in Real-Time Monitoring Systems

Examples:

• Heart rate monitoring
  
• Server performance tracking
  
• Environmental sensors
  

Domain defines acceptable input ranges; alerts trigger when outputs exceed expected range.

Error Propagation Related to Domain and Range

Invalid domain values can cause:

• Mathematical exceptions
  
• Software crashes
  
• Model instability
  

Defensive programming always checks domain validity first.

Advanced Notation for Domain and Range

Interval Notation

• (-∞, ∞)
  
• [0, ∞)
  

Builder Notation

• {x | x ≥ 0}
  

Advanced math and programming rely on precise notation to avoid ambiguity.

Visualization Best Practices for Domain and Range

To improve clarity:

• Shade domain on x-axis
  
• Highlight range on y-axis
  
• Use color coding
  
• Add axis labels clearly
  

These practices improve learning outcomes and engagement.

Graphing Tools and Technology Support

Modern tools simplify understanding:

• Desmos Graphing Calculator
• GeoGebra
• Python (Matplotlib, Seaborn)
• Excel and Google Sheets

Common Mistakes Students Make

• Confusing domain with range
• Ignoring graph breaks
• Assuming domain is always infinite
• Forgetting real-world constraints

Avoiding these mistakes builds strong analytical skills.

Domain and Range in Data Science and AI

In machine learning:

• Domain = input features
• Range = predicted outputs

For example:

• Domain: Customer age, income
• Range: Purchase probability

This makes domain and range of a graph foundational in analytics modeling.

Summary and Key Takeaways

• Domain refers to all valid input values
• Range refers to all possible output values
• Graphs visually represent relationships
• Real-world systems always have constraints
• Understanding domain and range improves analytical thinking

Final Thought

Mastering the domain and range of a graph is not just about passing exams—it builds the foundation for logic, reasoning, data science, and AI-driven decision-making. With practice and visualization, this concept becomes intuitive and powerful.

FAQ’s