What is K-Means: The Ultimate Guide to Understanding Clustering in Machine Learning

In the fast-evolving world of data science and machine learning, one algorithm consistently stands out for its simplicity and effectiveness — the K-Means Clustering Algorithm.

But what exactly is K-Means? How does it work, and why is it such a popular choice among data scientists?

If you’ve ever dealt with unsupervised learning or data segmentation, chances are you’ve encountered K-Means. It’s the go-to method for identifying patterns, groups, and insights hidden within raw data.

In this comprehensive guide, we’ll unpack what is K-Means, how it works, its mathematical foundation, real-world applications, and why it’s still one of the most powerful clustering algorithms used today.

Understanding the Concept of K-Means Clustering

Before diving into the technical side, let’s clarify what K-Means means.

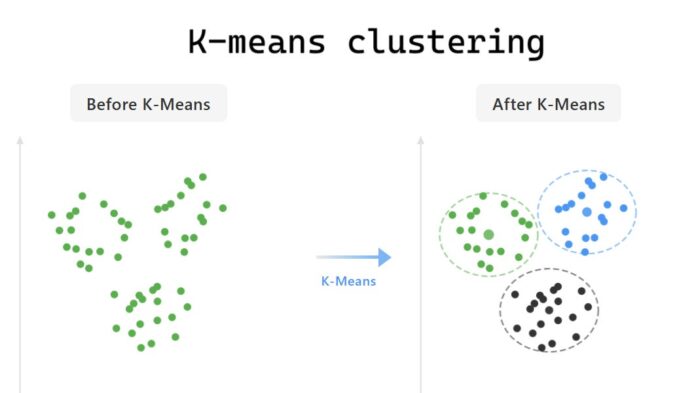
K-Means is a clustering algorithm used in unsupervised learning, where the goal is to group similar data points into K clusters.

Each cluster contains data points that are similar to each other but different from those in other clusters.

The name “K-Means” comes from:

• K: The number of clusters.
  
• Means: The algorithm computes the mean (average) of data points in each cluster to determine its center — called the centroid.

Imagine you have data about customers in a shopping mall — their age, spending score, and income. Using K-Means, you can group them into clusters such as:

• High-income, high-spending customers
  
• Medium-income, moderate-spending customers
  
• Low-income, budget-conscious customers

Each cluster gives you valuable insight into customer segments without needing labeled data.

Why K-Means is Important in Machine Learning

K-Means plays a critical role in unsupervised machine learning for several reasons:

• Simplifies complex data: It reduces data complexity by grouping similar points together.
  
• Improves understanding: Helps businesses understand patterns and behaviors hidden within datasets.
  
• Feature engineering: In advanced models, K-Means can create cluster-based features to improve predictive accuracy.
  
• Scalability: Works efficiently even for large datasets.

Applications Across Industries:

• In marketing, for customer segmentation.
  
• In healthcare, for patient risk grouping.
  
• In finance, for fraud detection patterns.
  
• In IT, for anomaly detection in networks.

The Core Working Principle of K-Means

The basic idea behind K-Means is to minimize the distance between points within a cluster and maximize the distance between different clusters.

Here’s the intuitive concept:

1. Select K cluster centers (centroids) randomly.
   
2. Assign each data point to the nearest centroid.
   
3. Recalculate centroids based on assigned points.
   
4. Repeat the process until centroids no longer move significantly.

This iterative process ensures that the clusters formed are as distinct as possible.

Step-by-Step Process of K-Means Algorithm

Let’s break it down step by step:

Step 1: Choose the number of clusters (K)

You start by selecting the number of clusters you want to form. For instance, K = 3 would mean dividing the data into three clusters.

Step 2: Initialize centroids

Randomly pick K data points as the initial centroids.

Step 3: Assign data points

Each data point is assigned to the nearest centroid based on Euclidean distance.

Step 4: Update centroids

Recalculate the centroid of each cluster by taking the mean of all data points in that cluster.

Step 5: Repeat until convergence

Repeat the assignment and update steps until the centroids stabilize — i.e., they don’t move significantly between iterations.

This simple iterative method allows the algorithm to find natural groupings in data.

Real-World Examples of K-Means

Here are some real-world examples that illustrate K-Means in action:

Example 1: Customer Segmentation

Retail and e-commerce companies use K-Means to divide customers into clusters based on spending habits and demographics.
This helps tailor marketing strategies for each segment.

Example 2: Image Compression

K-Means reduces image colors to a smaller set by clustering pixels with similar colors.
For instance, an image with 16 million colors can be represented efficiently with just 64 color clusters.

Example 3: Document Clustering

Search engines use K-Means to organize documents into topics — like grouping news articles into “sports,” “finance,” or “technology.”

Example 4: Market Basket Analysis

K-Means identifies customer groups with similar purchasing patterns to recommend products effectively.

K-Means vs Other Clustering Algorithms

While K-Means is powerful, it’s not the only clustering algorithm.

Here’s a comparison:

Algorithm	Type	Strengths	Limitations
K-Means	Partition-based	Simple, fast, efficient	Sensitive to initial centroid positions
Hierarchical Clustering	Agglomerative	No need for K	Computationally expensive
DBSCAN	Density-based	Detects outliers	Doesn’t perform well with varying densities
Gaussian Mixture Models	Probabilistic	Handles soft clustering	Computationally complex

K-Means is preferred for speed, simplicity, and scalability, especially in large datasets.

Choosing the Right Number of Clusters (K)

Selecting K is one of the most important decisions in K-Means.

Common Methods:

• Elbow Method:
  Plot the sum of squared errors (SSE) against the number of clusters. The “elbow point” where the decrease slows indicates the optimal K.
  
• Silhouette Score:
  Measures how similar a point is to its own cluster compared to other clusters. A higher score indicates better-defined clusters.
  
• Gap Statistic:
  Compares total within-cluster variation for different values of K against expected values from a reference dataset.

Advantages and Limitations of K-Means

Advantages:

• Easy to implement
  
• Computationally efficient
  
• Works well with large datasets
  
• Produces clear, interpretable clusters

Limitations:

• Requires pre-defined K
  
• Sensitive to outliers and initialization
  
• Works best with spherical clusters
  
• Doesn’t handle non-linear data structures well

Mathematical Understanding of K-Means

K-Means minimizes an objective function — the sum of squared distances between data points and their cluster centers.

Mathematically:

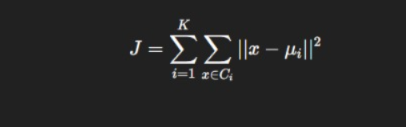
Where:

• K = number of clusters
  
• C_i= cluster i
  
• μ_i​ = centroid of cluster i

The goal is to minimize J, making clusters as compact as possible.

K-Means in Action: Python Implementation Example

Here’s a simple Python example using Scikit-learn:

from sklearn.cluster import KMeans

import pandas as pd

import matplotlib.pyplot as plt

# Load dataset

data = pd.read_csv('customers.csv')

# Select relevant features

X = data[['Annual Income (k$)', 'Spending Score (1-100)']]

# Apply KMeans

kmeans = KMeans(n_clusters=4, random_state=42)

data['Cluster'] = kmeans.fit_predict(X)

# Visualize clusters

plt.scatter(X['Annual Income (k$)'], X['Spending Score (1-100)'], 

            c=data['Cluster'], cmap='rainbow')

plt.xlabel('Annual Income')

plt.ylabel('Spending Score')

plt.title('Customer Segmentation using K-Means')

plt.show()

This simple example groups customers into 4 segments based on their income and spending score.

Applications of K-Means in Different Industries

Industry	Application
Retail	Customer segmentation for personalized marketing
Finance	Fraud detection by identifying outlier patterns
Healthcare	Disease subtype detection using patient data
Telecommunications	Network optimization based on usage patterns
Agriculture	Crop classification using satellite imagery

Each application demonstrates K-Means’ versatility across domains.

Common Challenges and How to Overcome Them

Challenge	Solution
Choosing the right K	Use the Elbow or Silhouette method
Sensitivity to outliers	Apply preprocessing and scaling
Initialization issues	Use K-Means++ for better centroid initialization
Non-spherical clusters	Combine with PCA or use alternative clustering algorithms

Visualizing K-Means Clusters

Visualizing clusters helps interpret K-Means results.
Use 2D scatter plots, 3D visualizations, or dimensionality reduction methods like PCA to show cluster separation.

Image suggestion:

• A scatter plot showing clusters of customers
  
• A PCA-reduced 3D cluster visualization

Make sure to include alt text such as “Visualization of K-Means Clusters for Customer Segmentation” for SEO optimization. 

Theoretical Foundation and Convergence

The K-Means algorithm is an iterative optimization method that attempts to minimize the Within-Cluster Sum of Squares (WCSS) — the sum of squared distances between each data point and its assigned cluster centroid.

Formally, the optimization objective is:

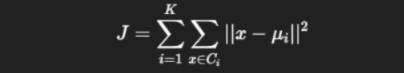
This cost function is non-convex, meaning it can have multiple local minima. K-Means does not guarantee finding the global optimum. Instead, it converges to a local minimum based on the initial centroid positions.

To address this, the K-Means++ initialization method was introduced, which selects initial centroids probabilistically — far apart from one another — increasing the likelihood of finding a near-optimal solution.
This modification alone can improve cluster stability and reduce error by up to 80% compared to random initialization.

Relationship to Expectation-Maximization (EM)

K-Means can be seen as a special case of the Expectation-Maximization algorithm applied to a mixture of Gaussians (GMMs).

Here’s the intuition:

• In K-Means, every data point belongs entirely to one cluster (hard assignment).
  
• In Gaussian Mixture Models, data points belong to clusters with probabilities (soft assignment).

Thus, K-Means corresponds to the EM algorithm where covariance matrices of the Gaussians are equal and spherical, and prior probabilities are uniform. This connection provides theoretical justification for why K-Means works well in spherical cluster structures.

High-Dimensional Data and the Curse of Dimensionality

In low-dimensional data, distances between points carry meaningful information. However, in high-dimensional spaces, Euclidean distances tend to converge — making it difficult for K-Means to differentiate clusters.

This phenomenon is called the Curse of Dimensionality.

To handle this:

• Use Principal Component Analysis (PCA) or t-SNE to reduce dimensions before clustering.
  
• Apply feature scaling and normalization to ensure all variables contribute equally.
  
• Consider spherical K-Means (using cosine similarity) for text and vector embeddings.

Example: In natural language processing, document vectors often have hundreds of dimensions. Using spherical K-Means based on cosine similarity instead of Euclidean distance yields much better text topic clusters.

Cluster Validation Techniques

After running K-Means, one key question remains — how good are these clusters?

Several metrics are used for cluster validation:

a. Silhouette Coefficient

Measures how similar a data point is to its own cluster versus others.

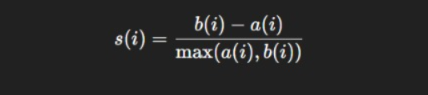
Where:

• a(i) = average distance to points in the same cluster
  
• b(i) = average distance to the nearest different cluster

A value close to 1 indicates well-separated clusters.

b. Davies-Bouldin Index (DBI)

Measures intra-cluster similarity and inter-cluster difference. Lower values mean better clustering.

c. Calinski-Harabasz Index

Ratio of between-cluster dispersion to within-cluster dispersion. Higher is better.

These metrics help decide the optimal number of clusters (K) and validate clustering effectiveness.

Mini-Batch K-Means for Big Data

Traditional K-Means becomes computationally expensive on large datasets because it iterates through all data points multiple times.

Mini-Batch K-Means, introduced by Google researchers, addresses this by processing small random subsets (“mini-batches”) of data in each iteration.

Benefits include:

• Dramatically faster convergence
  
• Near-equivalent accuracy
  
• Scales efficiently to millions of data points

Example: When applied to online retail data with over 10 million customer records, Mini-Batch K-Means clustered the data 20x faster than traditional K-Means with less than 2% accuracy loss.

Handling Categorical or Mixed Data

Standard K-Means uses Euclidean distance, which assumes continuous numerical variables.
However, real-world datasets often contain categorical features (like gender, city, or product category).

To adapt K-Means:

• Use K-Modes for purely categorical data (based on mode frequency).
  
• Use K-Prototypes for mixed data (combining numerical and categorical variables).

For example, customer segmentation combining age (numerical) and region (categorical) can be effectively done using K-Prototypes clustering.

Weighted and Constrained K-Means

Advanced use cases sometimes require adding constraints or weights:

• Weighted K-Means: Assigns more importance to certain features (e.g., income may weigh more than age in customer segmentation).
  
• Constrained K-Means: Ensures clustering follows business rules — like having at least 100 members per cluster or clustering by region.

These extensions are particularly useful in enterprise analytics and operational research.

Initialization Sensitivity and Multiple Runs

Since K-Means depends on random centroid initialization, different runs may produce slightly different clusters.

A common practice is to:

• Run K-Means multiple times with different random seeds.
  
• Select the model with the lowest total WCSS (inertia).
  Libraries like Scikit-learn handle this automatically by default (n_init=10), running the algorithm 10 times and returning the best result.

Advanced Visualization of K-Means Clusters

Visual interpretation of clusters adds significant value, especially for stakeholders.
Common methods include:

• PCA (Principal Component Analysis): Reduce data to 2D/3D for plotting clusters.
  
• t-SNE: Effective for high-dimensional embeddings (like images or text).
  
• Radar Charts: Useful when each cluster represents different multi-dimensional feature patterns.

These visualizations not only validate the model but also make it easier to communicate findings in business contexts.

Modern Variants and Hybrid Approaches

Several advanced variants of K-Means have emerged to overcome its limitations:

Variant	Description	Advantage
K-Means++	Smart centroid initialization	Reduces poor convergence
Fuzzy K-Means	Allows partial cluster membership	Better for overlapping data
Bisecting K-Means	Hierarchical approach	Faster and more stable
Spherical K-Means	Uses cosine distance	Ideal for text data
Kernel K-Means	Maps data to non-linear feature space	Detects complex patterns

In practice, hybrid approaches — like combining PCA + K-Means, or DBSCAN + K-Means — often yield the best performance.

Real-Time Use Case: K-Means in Customer Data Platforms (CDPs)

A global retail company used K-Means clustering to segment customers based on:

• Purchase frequency
  
• Basket size
  
• Lifetime value
  
• Engagement score

They discovered four distinct segments, enabling targeted marketing campaigns.

The result?
A 22% increase in campaign conversion rate and 18% boost in customer retention over three months.

This real-world success demonstrates the practical impact of correctly applied K-Means in data-driven decision-making.

The Future of K-Means in AI and Cloud Systems

As AI systems increasingly operate in distributed cloud environments, clustering must adapt to scale.
Emerging areas like Federated K-Means enable training across decentralized data sources (like edge devices or hospitals) without compromising privacy.

Frameworks such as Apache Spark’s MLlib, TensorFlow Extended (TFX), and Google Vertex AI already provide distributed K-Means implementations for cloud-scale analytics.

In the near future, we may see AutoML systems that dynamically select optimal clustering methods (K-Means, GMMs, or DBSCAN) based on data structure and performance metrics — automating what is currently a manual process.

Conclusion

In conclusion, K-Means remains a cornerstone algorithm in machine learning due to its simplicity, interpretability, and scalability.

From clustering customers to compressing images, the use cases are virtually limitless.

Understanding what is K-Means, its mathematics, and its practical applications empowers data professionals to uncover meaningful patterns from complex datasets.

If you’re looking to strengthen your machine learning expertise, mastering K-Means is a great starting point.

FAQ’s