In today’s data-driven world, organizations collect vast amounts of data with numerous variables. While this high-dimensional data can contain valuable insights, it often becomes complex to analyze and visualize. Principal Component Analysis (PCA) is a powerful statistical technique used to simplify such datasets while preserving their core information.
PCA helps reduce the number of variables in your data (dimensionality reduction) while retaining the most important patterns. This makes it easier for analysts and machine learning models to interpret the data efficiently.
What is PCA?
Principal Component Analysis (PCA) is a mathematical technique used to reduce the number of variables in a dataset while retaining the maximum amount of information. It transforms high-dimensional data into a smaller set of new variables called principal components, which capture the major patterns and variation in the data.
PCA is widely used when:
- There are too many features.
- Features are correlated.
- Visualization of multidimensional data is required.
- Machine learning models need to be optimized for performance.
How Does PCA Do That?
PCA works through a series of mathematical steps designed to identify the directions where the dataset varies the most. These high-variance directions become the new axes (principal components).
PCA achieves dimensionality reduction by:
- Measuring relationships between variables through a covariance matrix.
- Finding eigenvectors and eigenvalues, which describe new directions of maximum variance.
- Ranking components by how much information (variance) they capture.
- Projecting original data onto a smaller number of principal components.
In simple terms:PCA rotates the coordinate system so that the data spreads out as much as possible along new axes.
Why Principal Component Analysis is Important in Data Science
Data science projects often deal with hundreds or even thousands of features. High-dimensional data can cause:
- Computational inefficiency – Slower processing time.
- Overfitting – Too many variables increase model complexity.
- Difficulty in visualization – More than three dimensions are hard to plot.
By applying Principal Component Analysis, you can:
- Compress large datasets without losing significant accuracy.
- Improve machine learning model performance.
- Make data visualization possible in 2D or 3D.
How Principal Component Analysis Works – The Step-by-Step Process
The PCA process involves mathematical transformations to identify the directions (principal components) where data variation is maximum.
Steps in PCA:
- Standardize the data – Ensure all variables have equal weight by normalizing them.
- Calculate the covariance matrix – Understand relationships between variables.
- Compute eigenvectors and eigenvalues – Identify directions of maximum variance.
- Sort components by explained variance – Keep the most important ones.
- Transform the dataset – Project original data onto the principal components.
How Principal Component Analysis Works
Here is the workflow behind PCA broken down into intuitive steps:
1. Standardize the Data
Ensures all features have equal influence.
Variables with large numerical ranges won’t dominate.
2. Compute the Covariance Matrix
Shows how variables vary with respect to each other:
- Positive covariance → variables increase together
- Negative covariance → inverse relationships
3. Calculate Eigenvalues and Eigenvectors
- Eigenvectors = directions of maximum variance
- Eigenvalues = magnitude of variance captured
4. Sort Principal Components
Components are ranked by explained variance:
- PC1 → captures the highest variance
- PC2 → captures the next highest (independent of PC1), and so on
5. Transform the Data
Project the dataset onto the selected principal components.
This gives a simplified version of the data with minimal information loss.
Calculating Principal Components
Principal components are calculated by applying linear algebra operations:
Formula Representation
Each principal component is a linear combination of original variables:
PC1=a1X1+a2X2+…+anXn
Where:
- a1,a2,…,an = loadings (weights from eigenvectors)
- X1,X2,…,Xn = standardized original features
Steps:
- Compute eigenvalues/eigenvectors of the covariance matrix.
- Select top k eigenvectors (based on largest eigenvalues).
- Form a projection matrix.
- Multiply the original dataset by this matrix.
This gives the reduced-dimension dataset.
Visualizing High-Dimensional Data using PCA
Since human vision is limited to 2D and 3D, PCA helps convert complex datasets into:
- 2D scatter plots
- 3D visualizations
- Cluster visualizations
- Feature-space reduction maps
Visualization helps identify:
- Group patterns
- Hidden clusters
- Non-obvious correlations
- Outliers
- Decision boundaries
PCA is commonly used in:
- Customer segmentation charts
- Genetic expression visualization
- Image recognition feature maps
Noise Reduction and Signal Enhancement
PCA is highly effective in denoising data.
How PCA reduces noise:
- Noise typically spreads across many components.
- Important signal is concentrated in the first few components.
- By retaining only components with high variance, PCA removes low-variance noise.
Applications:
- Speech recognition
- ECG/EEG signal processing
- Image denoising
- Removing sensor-based environmental noise
Example:
Keeping the first 10 components of a 200-feature dataset may remove 90% of noise while preserving meaningful structure.
Understanding PCA Through Geometric Interpretation
PCA can be visualized geometrically:
- Each data point exists in an n-dimensional space.
- PCA rotates this coordinate system to find the axes of maximum variance.
- These new axes are orthogonal (at right angles).
- Projecting data onto these axes preserves the most meaningful structure.
This geometric shift simplifies complex data into its essential shape.
Correlation vs. Covariance in PCA
PCA can be computed using either:
Covariance Matrix PCA
- Best when variables are on similar scales.
- Sensitive to magnitude differences.
Correlation Matrix PCA
- Used when variables have different units (e.g., age vs. income).
- Standardizes automatically.
Rule of thumb:
If variable scales differ → use correlation matrix.
If all variables are already normalized → use covariance matrix.
Explained Variance and the Scree Plot
To decide how many principal components to keep:
Explained Variance Ratio
Shows how much information each component captures.
For example:
- PC1 = 62% variance
- PC2 = 18% variance
- PC3 = 9% variance
PC1 + PC2 = 80% → good for 2D visualization.
Scree Plot
A graph showing eigenvalues in decreasing order.
Look for:
- The “elbow point”—after which extra PCs contribute little.
This provides a data-driven approach to dimensionality reduction.
When Should You Not Use PCA?
Even though PCA is powerful, avoid using it when:
- Data is non-linear (use t-SNE, UMAP instead).
- Original features must remain interpretable.
- The dataset contains categorical variables that can’t be meaningfully projected.
- Variance does not represent importance (e.g., NLP text vectors).
PCA is not a one-size-fits-all tool and should be selected based on the data structure.
PCA for Feature Engineering
PCA can generate new synthetic features:
- Create PC1, PC2, PC3…
- Replace original features with these new ones.
- These PCs can serve as compact, noise-free features for ML models.
Example:
In credit scoring, 30+ financial features can be reduced into 5–10 meaningful components.
PCA for Outlier Detection
PCA helps detect outliers by:
- Identifying data points far from cluster centers in PC space.
- Creating PCA-based anomaly scores (distance metrics like Mahalanobis distance).
This is widely used in:
- Fraud detection
- Quality inspection
- IoT sensor anomaly detection
Pitfalls and Misconceptions of PCA
Common mistakes include:
1. Skipping Standardization
If features are not normalized:
- Large-scale features dominate PC1
- Results become misleading
2. Misinterpreting Principal Components
PCs are linear combinations—not real-world variables.
3. Using Too Many PCs
Using all PCs defeats the purpose of reduction.
4. Assuming PCA Improves Accuracy
PCA may reduce model performance if:
- Key information lies in lower variance components
- The problem is non-linear
Real-World Case Studies Where PCA Excels
A. Face Recognition (Eigenfaces)
PCA creates “eigenfaces”—principal components of human facial features.
Used in:
- Face identification
- Surveillance systems
B. Stock Market Trend Analysis
PCA identifies major underlying factors such as:
- Market momentum
- Interest rate influence
- Sector performance
C. Gene Expression Analysis
Reduces thousands of gene variables to a few interpretable biological factors.
D. Customer Segmentation
Retailers use PCA to condense hundreds of customer attributes:
- Purchasing frequency
- Income range
- Buying behavior
- Product preferences
PCA vs SVD (Singular Value Decomposition)
PCA is tightly connected with SVD.
PCA uses:
- Covariance → eigen decomposition
SVD uses:
- Data matrix → UΣVᵀ decomposition
SVD is:
- More stable
- Faster
- Works better with high-dimensional data
Most machine learning libraries actually use SVD to compute PCA internally.
PCA for Machine Learning Pipeline Optimization
PCA helps ML pipelines by:
- Reducing overfitting
- Improving generalization
- Speeding up training time
- Handling multicollinearity
Models that benefit the most:
- Logistic Regression
- SVM
- KNN
- Linear Regression
Deep learning models usually skip PCA because they learn feature reduction internally.
High-Dimensional Visualization Techniques Complementing PCA
Use PCA in combination with:
t-SNE
For non-linear structure visualization.
UMAP
Faster than t-SNE, captures global + local structure.
MDS
For distance-preserving projections.
Autoencoders
Neural networks for non-linear reduction.
Mathematical Intuition Behind Principal Component Analysis
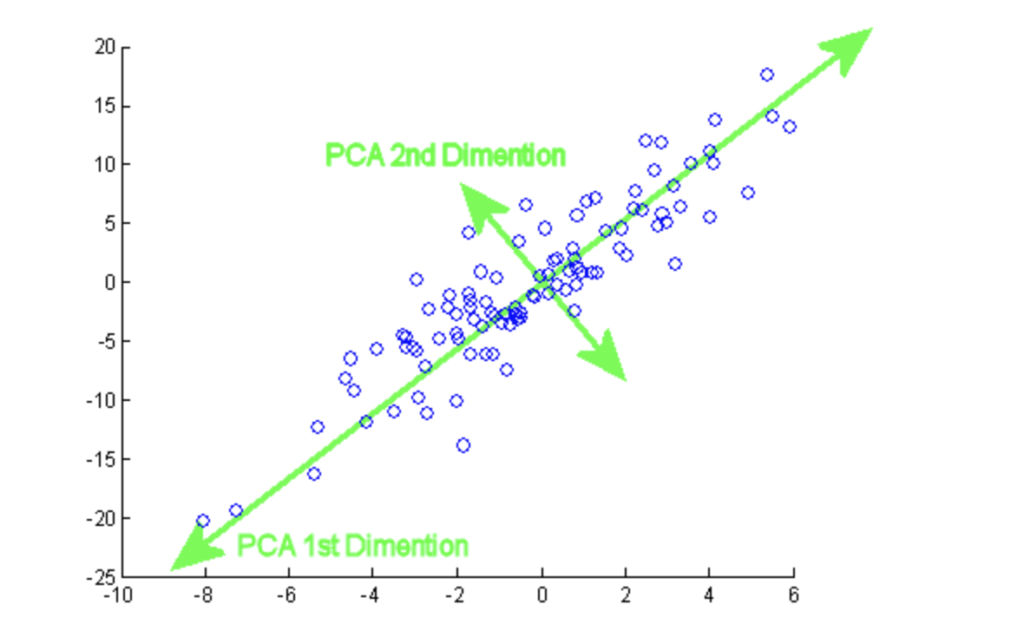
The heart of PCA lies in linear algebra. Each principal component is a linear combination of the original variables.
- Covariance Matrix shows how variables change together.
- Eigenvectors determine the direction of principal components.
- Eigenvalues represent the magnitude of variance captured.
For instance, in a dataset with two variables — height and weight — PCA may find that most variation lies along a single line representing general body size.
Key Terminologies in PCA
- Principal Components – New variables created from original data.
- Explained Variance – Amount of information retained by each component.
- Dimensionality Reduction – Reducing features while preserving essential patterns.
- Loading Scores – Correlation between original variables and principal components.
Advantages of Using Principal Component Analysis
- Simplifies high-dimensional datasets.
- Reduces computation time for algorithms.
- Removes multicollinearity in data.
- Enhances visualization possibilities.
Limitations of Principal Component Analysis
- PCA is a linear technique – may not work well with non-linear relationships.
- Components are not easily interpretable.
- Sensitive to variable scaling.
Real-World Applications of PCA
- Image Compression – Reducing image size without losing significant detail.
- Finance – Identifying main factors driving stock prices.
- Healthcare – Simplifying patient data for disease prediction.
- Marketing – Understanding customer segmentation.
Principal Component Analysis vs Other Dimensionality Reduction Techniques
| Feature | PCA | t-SNE | LDA |
| Approach | Linear | Non-linear | Supervised |
| Interpretability | Moderate | Low | High |
| Speed | High | Medium | Medium |
| Best Use Case | Large, linear datasets | Visualization | Classification |
PCA Implementation in Python (Step-by-Step)
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# Load dataset
data = pd.read_csv("dataset.csv")
# Standardize the features
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data)
# Apply PCA
pca = PCA(n_components=2)
pca_result = pca.fit_transform(scaled_data)
# Create a DataFrame
pca_df = pd.DataFrame(pca_result, columns=['PC1', 'PC2'])
print(pca.explained_variance_ratio_)
Explanation:
- Data is standardized to ensure fair comparison.
- PCA reduces the dataset to 2 components for visualization.
Best Practices for Using PCA Effectively
- Always standardize or normalize data before PCA.
- Use scree plots to decide the number of components.
- Interpret results in the context of domain knowledge.
- Combine PCA with machine learning models for efficiency.
Conclusion
Principal Component Analysis is a cornerstone of data science and analytics. By reducing dimensionality while preserving valuable insights, it allows for faster computations, improved model performance, and better visual understanding.Whether in finance, healthcare, or machine learning, PCA continues to be a go-to technique for transforming complex datasets into actionable insights.
FAQ’s
What is principal component analysis?
Principal Component Analysis (PCA) is a statistical dimensionality reduction technique that transforms high-dimensional data into a smaller set of uncorrelated components while preserving the most important patterns and variance in the dataset.
Is PCA outdated?
No, PCA is not outdated—it’s still widely used as a fast, reliable, and interpretable dimensionality reduction technique, especially for preprocessing, noise reduction, and visualization in modern machine learning workflows.
Is PCA a black box?
No, PCA is not a black box—its transformations are fully transparent and mathematically interpretable, allowing you to clearly understand how each principal component is formed from the original features.
Is PCA part of AI?
Yes, PCA is part of the broader AI and machine learning toolkit—it’s commonly used for feature reduction, preprocessing, noise removal, and improving model performance in AI pipelines.
Is PCA a generative model?
No, PCA is not a generative model—it’s a linear dimensionality reduction technique that transforms data but does not generate new samples like true generative models do.
