Unlocking Complex Patterns with Hierarchical Cluster Analysis in Modern Data Science

Data today is generated at an unprecedented scale. Businesses, researchers, and AI systems constantly process large volumes of structured and unstructured data. Extracting meaningful patterns from this data requires intelligent techniques.

Cluster analysis is one such method that groups similar data points together based on defined similarity measures. Unlike supervised learning, clustering does not rely on labeled outputs. Instead, it identifies hidden patterns naturally present in the data.

Among clustering techniques, hierarchical cluster analysis stands out for its interpretability and flexibility.

What is Hierarchical Cluster Analysis?

Hierarchical cluster analysis is an unsupervised machine learning technique that builds nested clusters by either merging or splitting them successively. The result is a tree-like structure called a dendrogram that visually represents relationships between observations.

Unlike K-Means clustering, this method does not require pre-specifying the number of clusters. That flexibility makes it particularly powerful for exploratory data analysis.

Hierarchical clustering is widely used in:

• Market segmentation
• Genomics research
• Document classification
• Image recognition
• Customer behavior analytics

Why Hierarchical Cluster Analysis Matters in Modern Data Science

Modern AI systems increasingly rely on pattern recognition and similarity modeling. From recommendation engines to anomaly detection systems, grouping similar items is fundamental.

Hierarchical cluster analysis provides:

• Structured visualization of data relationships
• No need to define cluster count initially
• Interpretability through dendrograms
• Flexibility across multiple distance metrics

In business intelligence platforms, clustering supports decision-making in marketing, finance, and healthcare analytics.

If you have previously read our blog on K-Means clustering, you may notice that hierarchical clustering does not depend on centroid initialization, which reduces instability caused by random seeds.

Types of Hierarchical Clustering

There are two primary approaches.

Agglomerative Hierarchical Clustering

This is a bottom-up approach.

• Each data point starts as its own cluster
• The closest clusters are merged step by step
• The process continues until all points form a single cluster

This is the most commonly used method.

Divisive Hierarchical Clustering

This is a top-down approach.

• All data points begin in one cluster
• The cluster is split recursively
• Splitting continues until each point stands alone

Divisive methods are computationally intensive but useful in specific research domains.

Key Concepts Behind Hierarchical Cluster Analysis

Distance Metrics

Distance defines similarity. Common distance measures include:

• Euclidean distance
• Manhattan distance
• Cosine similarity
• Minkowski distance

For high-dimensional datasets such as text embeddings, cosine similarity is often more appropriate.

Linkage Criteria

Linkage determines how clusters are merged.

• Single linkage: minimum distance between cluster points
• Complete linkage: maximum distance
• Average linkage: average distance
• Ward’s method: minimizes variance within clusters

Ward’s method is widely used because it tends to produce compact clusters.

Dendrogram

A dendrogram visually represents hierarchical clustering.

The dendrogram helps determine:

• Optimal number of clusters
• Distance threshold
• Cluster hierarchy structure

Mathematical Foundations

At its core, hierarchical cluster analysis relies on pairwise distance matrices.

If we denote data points as xi and xj, the Euclidean distance is:

d(xi, xj) = √Σ(xik − xjk)²

For Ward’s method, the objective is minimizing the increase in total within-cluster variance after merging.

This variance minimization ensures homogeneous clusters.

Step-by-Step Process of Hierarchical Cluster Analysis

1. Standardize data
2. Compute distance matrix
3. Select linkage method
4. Merge clusters iteratively
5. Plot dendrogram
6. Cut dendrogram at desired level

This process ensures reproducibility and transparency.

Real-Time Business Applications

Customer Segmentation in Retail

An e-commerce company clusters customers based on:

• Purchase frequency
• Average order value
• Browsing behavior

Using hierarchical clustering, marketers identify high-value customers and target them with premium offers.

Healthcare Analytics

Hospitals group patients based on symptoms, test results, and genetic markers. This helps in disease subtype identification.

Financial Risk Modeling

Banks cluster loan applicants based on credit behavior. Risk patterns become easier to detect.

Document Classification

News articles are clustered based on textual similarity for automated categorization.

Hierarchical Cluster Analysis in Python

import pandas as pd

from scipy.cluster.hierarchy import linkage, dendrogram

import matplotlib.pyplot as plt

data = pd.read_csv("data.csv")

Z = linkage(data, method='ward')

plt.figure(figsize=(10, 7))

dendrogram(Z)

plt.title("Hierarchical Cluster Analysis Dendrogram")

plt.show()

Hierarchical Cluster Analysis in R

data <- read.csv("data.csv")

d <- dist(data, method = "euclidean")

hc <- hclust(d, method = "ward.D2")

plot(hc)

Mathematical Foundation of Hierarchical Cluster Analysis

While hierarchical cluster analysis is often introduced visually through dendrograms, its mathematical backbone is rooted in distance metrics, similarity functions, and linkage criteria.

Distance Metrics in Hierarchical Cluster Analysis

The choice of distance metric significantly influences clustering results. Some commonly used metrics include:

• Euclidean Distance

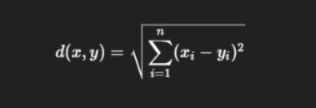
• Manhattan Distance

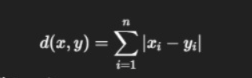
• Cosine Similarity (converted to distance)

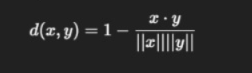
• Mahalanobis Distance
  Useful when features are correlated:

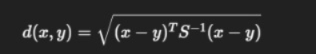
In real-world applications such as customer segmentation, Euclidean distance works well for standardized numeric features, while cosine similarity is more appropriate for text clustering.

Linkage Methods in Greater Detail

The linkage method determines how cluster distances are calculated during merging.

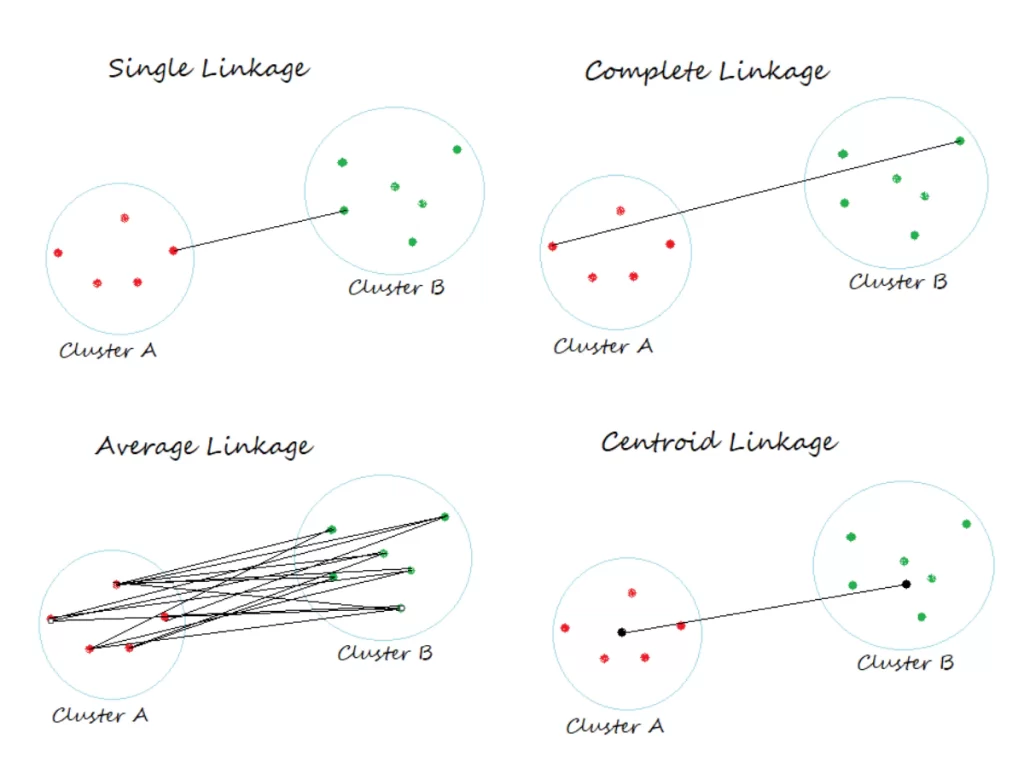
Single Linkage

• Uses minimum pairwise distance.
  
• Tends to produce elongated clusters.
  
• Sensitive to noise.
  
• Useful in detecting non-spherical cluster shapes.
  

Complete Linkage

• Uses maximum pairwise distance.
  
• Produces compact clusters.
  
• More resistant to chaining effects.
  

Average Linkage

• Uses average pairwise distance.
  
• Balanced between single and complete linkage.
  
• Common in bioinformatics.
  

Ward’s Method

• Minimizes within-cluster variance.
  
• Often produces well-separated spherical clusters.
  
• Frequently used in market research and social sciences.
  

Ward’s method is particularly useful when interpretability and cluster compactness are important.

Agglomerative vs Divisive: Algorithmic Perspective

Agglomerative Hierarchical Clustering

Bottom-up approach:

1. Start with n singleton clusters.
   
2. Compute pairwise distance matrix.
   
3. Merge closest clusters.
   
4. Update distance matrix.
   
5. Repeat until one cluster remains.
   

Time Complexity:

• O(n³) naive implementation
  
• O(n² log n) optimized
  

Divisive Hierarchical Clustering

Top-down approach:

1. Start with one cluster.
   
2. Split into subclusters.
   
3. Recursively split until desired structure is achieved.
   

Divisive methods are computationally more expensive but can sometimes yield better global structure.

Scalability Challenges in Large Datasets

Hierarchical cluster analysis struggles with very large datasets because:

• Distance matrix requires O(n²) memory.
  
• Merging operations increase computational cost.
  
• Not suitable for millions of data points without approximation.
  

Practical Solutions

• Use sampling techniques.
  
• Apply dimensionality reduction (PCA, t-SNE).
  
• Combine with K-Means for pre-clustering.
  
• Use parallelized implementations in Spark MLlib.
  

For large-scale clustering, hybrid approaches often outperform pure hierarchical clustering.

Dendrogram Interpretation at Expert Level

A dendrogram visualizes the clustering hierarchy.

Key interpretation points:

• Height of branches represents dissimilarity.
  
• Short vertical lines indicate similar clusters.
  
• Long vertical lines indicate distinct clusters.
  
• Cutting at different heights changes cluster granularity.
  

In healthcare analytics, dendrograms are used to group patients by symptom similarity. Cutting at different levels helps identify subtypes of diseases.

Real-Time Industry Applications

1. Healthcare: Disease Subtype Identification

Researchers cluster gene expression data to identify cancer subtypes. Hierarchical cluster analysis helps discover patterns that are not predefined.

2. E-Commerce: Product Recommendation

Products can be grouped based on purchase behavior. Customers purchasing similar products fall into the same cluster, improving recommendation engines.

3. Finance: Risk Profiling

Banks cluster customers based on transaction behavior, income level, and credit history to categorize risk levels.

4. Cybersecurity: Intrusion Detection

Network behavior patterns are clustered to detect abnormal activities.

5. Social Media Analytics

User engagement metrics are clustered to segment audience types for targeted advertising.

Comparison with Other Clustering Techniques

Method	Requires K	Scalable	Handles Noise	Hierarchical Structure
K-Means	Yes	High	Poor	No
DBSCAN	No	Moderate	Good	No
Hierarchical	No	Low	Moderate	Yes

Hierarchical cluster analysis is particularly valuable when:

• The number of clusters is unknown.
  
• A nested structure exists.
  
• Interpretability is important.
  

Preprocessing Best Practices

Before applying hierarchical clustering:

• Normalize or standardize features.
  
• Handle missing values.
  
• Remove outliers.
  
• Consider dimensionality reduction.
  

Improper preprocessing can distort cluster results significantly.

Python Implementation Example

from sklearn.cluster import AgglomerativeClustering

from sklearn.datasets import make_blobs

import matplotlib.pyplot as plt

X, y = make_blobs(n_samples=200, centers=3, random_state=42)

model = AgglomerativeClustering(n_clusters=3, linkage='ward')

labels = model.fit_predict(X)

plt.scatter(X[:,0], X[:,1], c=labels)

plt.title("Hierarchical Clustering Result")

plt.show()

This simple example demonstrates agglomerative clustering with Ward linkage.

R Implementation Example

data <- dist(iris[,1:4])

hc <- hclust(data, method="ward.D2")

plot(hc)

Hierarchical cluster analysis is widely supported in R’s statistical ecosystem.

Model Evaluation Techniques

Unlike supervised learning, clustering lacks ground truth labels.

Evaluation methods include:

• Silhouette Score
  
• Cophenetic Correlation Coefficient
  
• Davies-Bouldin Index
  
• Visual inspection of dendrogram
  

Silhouette score helps measure how well data points fit within clusters.

Hybrid Hierarchical Clustering Approaches

Modern data science workflows often combine:

• K-Means for initial grouping.
  
• Hierarchical clustering for structure refinement.
  
• Density-based clustering for noise handling.
  

This multi-step approach balances scalability and interpretability.

Common Mistakes to Avoid

• Using unscaled features.
  
• Ignoring linkage method impact.
  
• Overinterpreting dendrogram.
  
• Applying to extremely large datasets without optimization.
  
• Not validating cluster stability.
  

Cluster stability testing via bootstrapping can improve reliability.

Emerging Research Directions

• Hierarchical clustering for deep embeddings.
  
• Graph-based hierarchical clustering.
  
• Hierarchical clustering in reinforcement learning.
  
• Automated selection of linkage methods.
  
• Integration with neural network feature extraction.
  

Hierarchical structures are increasingly integrated with representation learning in modern AI systems.

Choosing the Right Distance Metric

Selecting a metric depends on data type:

• Numerical data: Euclidean
• Categorical data: Hamming distance
• Text embeddings: Cosine similarity

Data preprocessing significantly impacts clustering results.

Advantages of Hierarchical Cluster Analysis

• No need to predefine cluster count
• Produces hierarchy
• Interpretable visualization
• Works with various similarity measures

Limitations

• Computationally expensive for large datasets
• Sensitive to noise and outliers
• Once merged, clusters cannot be split in agglomerative method

For large-scale datasets, alternative methods like K-Means or DBSCAN may be more efficient.

Comparison with K-Means Clustering

Feature	Hierarchical	K-Means
Cluster count required	No	Yes
Interpretability	High	Moderate
Computational complexity	Higher	Lower
Visualization	Dendrogram	Centroids

For more foundational knowledge, refer to our internal guide on unsupervised learning techniques.

Evaluating Clustering Performance

Common evaluation metrics include:

• Silhouette Score
• Davies-Bouldin Index
• Calinski-Harabasz Index

Higher silhouette score indicates better separation.

Visualizing Clusters

In addition to dendrograms, visualization methods include:

• PCA projections
• t-SNE plots
• UMAP embeddings

Conclusion

Hierarchical cluster analysis is a powerful and interpretable clustering technique used across industries. Its ability to reveal nested relationships makes it particularly valuable for exploratory data analysis.

Whether you are analyzing customer behavior, genomic data, financial risk, or text corpora, hierarchical clustering provides a structured way to uncover hidden patterns.

Understanding distance metrics, linkage methods, and dendrogram interpretation is essential for producing reliable clustering outcomes.

As datasets grow more complex, mastering hierarchical clustering strengthens your analytical toolkit and supports data-driven decision-making

FAQ’s