Understanding Regression: Define Regression in Statistics and Machine Learning

In the fields of statistics and machine learning, the term regression holds significant importance. When professionals and students seek to define regression, they are typically referring to a type of predictive modeling technique that estimates the relationships among variables. At its core, regression helps us understand how the dependent variable changes when any one of the independent variables is varied.

How Do We Define Regression?

To define regression, we must consider it as a statistical method that models and analyzes the relationship between a dependent variable (also known as the outcome or target) and one or more independent variables (also called predictors or features). The primary goal is to establish a mathematical equation that can be used to predict or explain the dependent variable based on the input variables.

For example, if a company wants to predict future sales based on advertising budget, then regression can be used to find the relationship between ad spend (independent variable) and sales (dependent variable). Once you define regression in this context, it becomes a powerful tool for decision-making and forecasting.

Types of Regression

There are various types of regression models depending on the nature of the data and the relationship between variables. When you define regression, it’s important to understand these types:

1. Linear Regression:

This is the simplest and most widely used form of regression. It models the relationship between two variables by fitting a straight line. The formula is:

 Y=a+bX+ϵ

 Where:

• Y is the dependent variable,
  
• X is the independent variable,
  
• a is the intercept,
  
• b is the slope,
  
• ϵ epsilon is the error term.
  

2. Multiple Linear Regression:

This involves more than one independent variable. It is used when the outcome is influenced by several factors.

Y=a+b  1 ​  X  1 ​  +b  2 ​  X  2 ​  +…+b  n ​  X  n ​  +ϵ

3. Logistic Regression:

Though it’s called regression, logistic regression is used for classification problems. It predicts the probability of an event occurring, such as whether an email is spam or not.

4. Polynomial Regression:

This is used when the relationship between the dependent and independent variables is nonlinear.

5. Ridge and Lasso Regression

Ridge Regression

Ridge Regression is an extension of linear regression designed to handle problems of multicollinearity (when independent variables are highly correlated). It adds a regularization term to the cost function that penalizes large coefficient values, preventing overfitting.

The cost function for Ridge Regression is:

Here,

• λ is the regularization parameter that controls the penalty strength,
  
• βj​ represents model coefficients.

A higher λ\lambdaλ shrinks coefficients more aggressively, helping stabilize the model. Ridge regression is best used when all variables contribute to predicting the outcome but some are highly correlated.

6. Lasso Regression

Lasso (Least Absolute Shrinkage and Selection Operator) Regression also adds a penalty, but it uses the absolute value of the coefficients rather than their squares:

Unlike Ridge, Lasso can shrink some coefficients to zero, effectively performing feature selection. This makes it ideal for high-dimensional datasets where only a subset of predictors is truly important.

In short:

• Ridge Regression → reduces model complexity but keeps all variables.
  
• Lasso Regression → reduces complexity and performs feature selection.

7. Support Vector Regression (SVR)

Support Vector Regression extends the principles of Support Vector Machines (SVM) to regression tasks. Instead of trying to find a hyperplane that separates classes, SVR attempts to find a function that fits the data within a certain margin of tolerance (ε).

The SVR model aims to:

• Minimize the error below a predefined threshold.
  
• Keep the model as flat as possible, ensuring generalization.

SVR is powerful for:

• Handling nonlinear relationships using kernel functions (e.g., RBF, polynomial).
  
• Performing well in high-dimensional spaces where linear regression fails.

For example, in predicting housing prices where relationships between variables (like area, location, and amenities) are nonlinear, SVR can provide more accurate results than traditional regression models.

8. Decision Tree Regression

Decision Tree Regression uses a tree-like structure to model decisions and their possible outcomes. Instead of fitting a single equation, it splits data into branches based on feature values and makes predictions at leaf nodes.

Each split is determined by minimizing an error metric (e.g., Mean Squared Error). The model recursively divides the dataset, making it easy to interpret and visualize.

Advantages:

• Handles both linear and nonlinear data.
  
• No need for data normalization or scaling.
  
• Easy to interpret through tree visualization.

However, standalone decision trees are prone to overfitting, especially on small datasets, which is why ensemble methods like Random Forests are often used.

9. Random Forest Regression

Random Forest Regression is an ensemble learning technique that builds multiple decision trees and averages their predictions. Each tree is trained on a random subset of data and features (a process called bootstrapping).

This approach reduces overfitting and improves prediction accuracy.

Key Benefits:

• Highly accurate and robust.
  
• Works well for both numerical and categorical data.
  
• Automatically handles missing values and variable importance ranking.

Random Forests are widely used in finance (credit scoring), healthcare (disease prediction), and marketing (customer segmentation) because they balance interpretability and performance.

Regression Evaluation Metrics

To assess how well a regression model performs, several metrics are used:

Adjusted R-squared:
Modified version of R² that accounts for the number of predictors. It’s preferred when comparing models with different numbers of variables.

Mean Absolute Error (MAE):
Average of absolute differences between predicted and actual values.

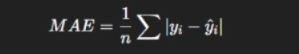
Mean Squared Error (MSE):
Measures average squared differences. Penalizes large errors.

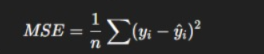
Root Mean Squared Error (RMSE):
Square root of MSE, useful for interpretability in original units.

R-squared (R²):

Represents how much variance in the dependent variable is explained by the model.

Higher values (closer to 1) indicate better model fit.

Why Define Regression?

When organizations and researchers define regression in their work, they unlock several benefits:

• Prediction: Regression models are widely used to make predictions in finance, marketing, healthcare, and many other domains.
  
• Insight: Regression helps identify key factors that influence an outcome, offering valuable insights for strategy and planning.
  
• Optimization: By understanding the relationships among variables, businesses can allocate resources more efficiently.

For example, in healthcare, regression models might predict patient recovery time based on age, treatment type, and initial diagnosis. In marketing, a company might use regression to predict customer lifetime value based on spending habits and demographic data.

Regression and Econometrics

Regression plays a central role in econometrics, the branch of economics that applies statistical and mathematical models to test hypotheses and forecast future trends. Econometrics relies heavily on regression analysis to quantify relationships between economic variables, such as income, consumption, inflation, and employment rates.

In econometrics, regression helps answer questions like:

• How does consumer spending change with income levels?
  
• What is the relationship between inflation and interest rates?
  
• How do education and experience influence wage growth?

Role of Regression in Econometrics

Econometricians use regression models to estimate causal relationships between variables while accounting for randomness or external influences. By doing so, they can isolate the effect of one variable on another.

For instance, a simple linear regression might model the relationship between household income (independent variable) and consumption (dependent variable):

Consumption=a+b(Income)+ϵ

Here, bbb (the slope) measures how much consumption changes for every unit change in income.

Applications in Econometrics

1. Policy Analysis: Governments use regression models to forecast the effects of fiscal or monetary policies.
   
2. Economic Forecasting: Analysts predict GDP growth, unemployment rates, or stock market trends.
   
3. Demand Estimation: Businesses estimate product demand based on price, marketing spend, and consumer demographics.
   
4. Causal Inference: Econometric regression helps determine cause-and-effect relationships, not just correlations.

Advanced econometric techniques often include multiple regression, time-series regression, and panel data models, which account for data over time or across entities like countries and companies.

Benefits of Regression Analysis

• Predictive Power: Enables accurate forecasting in domains like sales, finance, and healthcare.
  
• Interpretability: Regression coefficients provide insight into how each variable affects the outcome.
  
• Data-Driven Decision Making: Guides policy formulation and business strategies based on data patterns.
  
• Automation: Used in AI and ML pipelines to make continuous predictions in real-time.
  
• Flexibility: Works with both simple linear relationships and complex nonlinear data structures.

For example, companies use regression analysis to predict demand, optimize pricing, or estimate customer churn, empowering data-driven strategy development.

Limitations of Regression Analysis

Despite its power, regression analysis has certain limitations:

• Assumption Dependency: Linear regression assumes linearity, normal distribution, and homoscedasticity, which real-world data often violate.
  
• Outlier Sensitivity: Extreme values can distort model predictions significantly.
  
• Multicollinearity: Highly correlated variables can make coefficient estimation unstable.
  
• Overfitting Risk: Complex models (like polynomial regression) may perform well on training data but poorly on unseen data.
  
• Interpretation Challenges: Advanced models like Random Forest or SVR provide high accuracy but lack the transparency of simple linear models.

Understanding these limitations helps practitioners choose the right regression model and ensure robust, generalizable predictions.

Calculating Regression

At its core, calculating regression means finding the best-fit line that minimizes the difference between predicted and actual values. This process is achieved using the Least Squares Method, which minimizes the sum of squared residuals (errors).

Simple Linear Regression Calculation

The general equation of a regression line is:

Y=a+bX
Where:

• Y = Dependent variable
  
• X = Independent variable
  
• a = Intercept
  
• b = Slope (regression coefficient)

Steps to Calculate Regression

1. Collect Data: Gather paired values of X and Y.
   
2. Compute Means: Calculate the mean of both variables (Xˉ and Yˉ).
   
3. Calculate Slope (b):

1. Calculate Intercept (a):
   a=Yˉ−bXˉ
   Form the Regression Equation:
   Substitute a and b into the equation Y=a+bX.
   
2. Predict Outcomes: Use the regression equation to predict Y for given X values.

Interpretation

• The slope (b) shows the direction and strength of the relationship.
  
• The intercept (a) represents the expected value of Y when X=0.
  
• Residuals (differences between actual and predicted values) indicate the model’s accuracy — smaller residuals mean a better fit.

In machine learning, the same principle applies, though calculations are often automated using algorithms such as Ordinary Least Squares (OLS), Gradient Descent, or Regularization techniques like Ridge and Lasso regression.

Example of Regression Analysis in Finance

Regression analysis is a cornerstone of financial analytics and investment modeling. Financial professionals use regression to identify risk factors, predict returns, and optimize portfolios.

Example: Predicting Stock Returns

Let’s consider a regression model that predicts a stock’s future return (R_i​) based on market return (R_m):

R_i​=α+βR_m​+ϵ

• R_i​: Return of the individual stock
  
• R_m​: Return of the overall market index (e.g., S&P 500)
  
• α: The intercept or “alpha” — represents excess return independent of market performance
  
• β: The slope or “beta” — measures the stock’s sensitivity to market movements
  
• ϵ: Random error term

Interpretation:

• If β = 1, the stock moves in line with the market.
  
• If β > 1, the stock is more volatile (amplified risk and return).
  
• If β < 1, the stock is less volatile than the market.

For instance, if a regression analysis shows β=1.2, it means that when the market return increases by 1%, the stock is expected to increase by 1.2% on average.

Practical Applications in Finance

1. Portfolio Optimization: Identifying assets that provide the best risk-return trade-off.
   
2. Risk Management: Measuring exposure to market risk using beta coefficients.
   
3. Forecasting Returns: Estimating future prices or profits based on economic indicators.
   
4. Performance Evaluation: Determining if fund managers generate returns beyond market benchmarks (positive alpha).

Regression analysis thus serves as a powerful analytical engine in finance, connecting data-driven insights to investment decisions, market forecasting, and risk management strategies.

Applications of Regression

Once you define regression, it becomes clear how universally applicable it is:

• Economics: Forecasting economic indicators like inflation and GDP growth.
  
• Business Analytics: Predicting customer churn or sales trends.
  
• Environmental Science: Estimating pollution levels based on weather conditions.
  
• Real Estate: Predicting housing prices based on features like location, size, and age.
  

Best Practices When You Define Regression Models

• Data Preparation: Ensure the data is clean, with no missing or outlier values.
  
• Feature Selection: Choose relevant independent variables to improve model accuracy.
  
• Model Evaluation: Use metrics like R-squared, Mean Squared Error (MSE), or Root Mean Squared Error (RMSE) to evaluate performance.
  
• Avoid Overfitting: Make sure the model generalizes well to new data by not being overly complex.

Conclusion

To define regression is to understand a foundational concept that bridges the gap between data and decision-making. Whether you’re predicting future outcomes, identifying patterns, or testing hypotheses, regression provides the tools to analyze relationships between variables effectively. As data continues to shape industries across the globe, the ability to define regression and apply it correctly remains a crucial skill for data scientists, analysts, and business professionals alike.

FAQ’s