Every decision in data science involves uncertainty — from classifying a tumor as benign or malignant to deciding if a stock will rise or fall. In such uncertain environments, Bayesian Decision Theory stands as a guiding framework that allows us to make optimal decisions based on probability and prior knowledge.
Unlike deterministic systems that rely purely on rules or thresholds, Bayesian methods combine prior information, observed data, and cost or reward functions to deliver mathematically sound, data-driven decisions.
What is Bayesian Decision Theory?
At its core, Bayesian Decision Theory is a fundamental statistical approach to decision-making under uncertainty. It integrates the probabilistic reasoning of Bayes’ theorem with decision theory principles such as risk minimization.
This theory doesn’t just help in estimating probabilities — it helps in making the best possible decision given what is known (prior knowledge) and what is observed (data).
Key Idea:
Bayesian Decision Theory aims to minimize the expected loss (or maximize utility) by using probabilities derived from data.
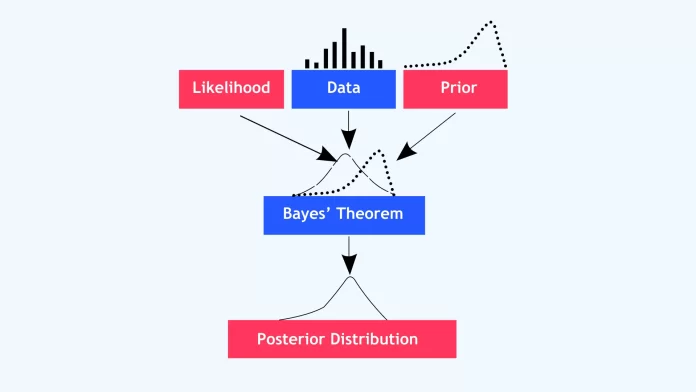
The Foundation: Bayes’ Theorem Explained
Before diving into Bayesian Decision Theory, it’s essential to understand Bayes’ theorem, the foundation of this approach.
The Bayes’ Formula:
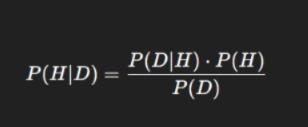
Where:
- P(H∣D) = Posterior probability (probability of hypothesis H given data D)
- P(D∣H) = Likelihood (probability of data given hypothesis)
- P(H) = Prior probability (initial belief before seeing data)
- P(D) = Evidence (total probability of data across all hypotheses)
Interpretation:
Bayes’ theorem updates our beliefs about a hypothesis based on new evidence. This updating process makes Bayesian methods highly adaptive and relevant in dynamic environments.
Key Components of Bayesian Decision Theory
Bayesian Decision Theory combines probabilities, actions, and loss functions to form a mathematical model of decision-making.
Main Components:
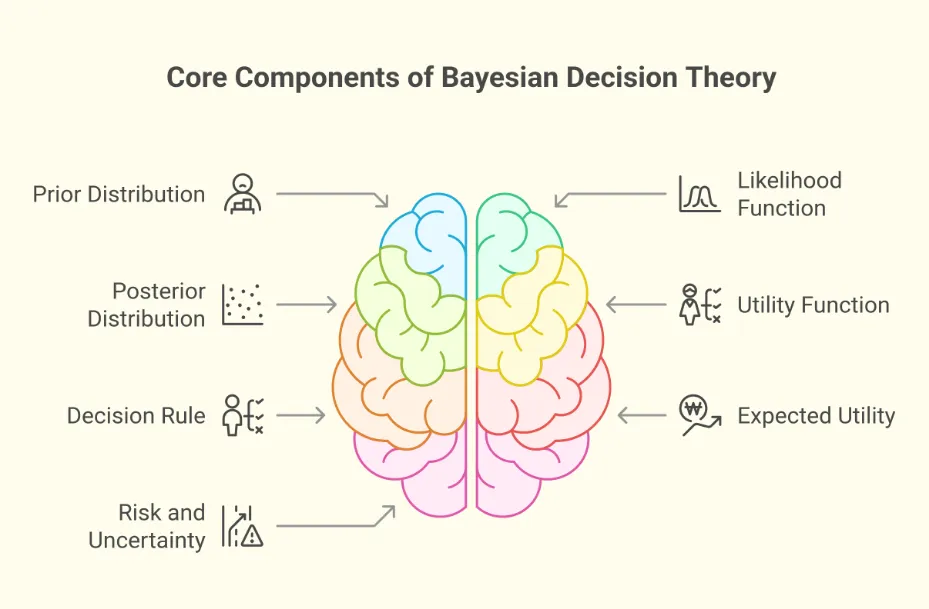
- Decision Space (A):
The set of all possible actions (e.g., approve a loan or reject it). - State of Nature (Θ):
Represents all possible real-world conditions that affect the outcome. - Loss Function (L(θ, a)):
Measures the cost of taking action a when the true state is θ. - Risk Function (R(θ, a)):
Expected loss averaged over all possible states. - Bayes Risk (r(a)):
The minimum expected loss achievable by an optimal decision rule.
The Role of Probability in Decision-Making
Probability acts as the backbone of Bayesian Decision Theory.
It quantifies uncertainty and provides a framework for rational reasoning.
Bayesian methods go beyond point estimates — they calculate full probability distributions, allowing better insights into risk, confidence, and uncertainty.
Example:
A weather forecasting model predicting rain tomorrow doesn’t just say “It will rain.”
Instead, it says, “There is a 70% probability of rain,” allowing planners to make informed, probabilistic decisions.
Loss Functions and Risk Analysis
Every decision has potential consequences — or losses — depending on the true state of the world. Bayesian Decision Theory incorporates these through loss functions.
Common Loss Functions:
- Zero-One Loss: Used in classification tasks (correct or incorrect decisions).
- Quadratic Loss: Used when errors increase exponentially with deviation.
- Asymmetric Loss: For decisions where false positives and false negatives have different costs (e.g., fraud detection).
Expected Risk:
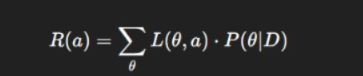
The decision rule is designed to minimize the expected risk — leading to rational, cost-sensitive outcomes.
Decision Boundaries and Classification
In machine learning, Bayesian Decision Theory defines decision boundaries — the thresholds where one class becomes more probable than another.
For example, in a spam classification model:
- If P(Spam∣Email)>P(NotSpam∣Email), classify as Spam.
- Otherwise, classify as Not Spam.
These probabilistic boundaries adapt based on data distribution, ensuring flexibility and accuracy.
Bayesian Decision Rule
The Bayesian Decision Rule states that for any observed data x, choose the action aia_iai that minimizes the posterior expected loss.
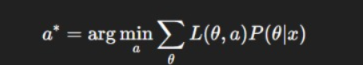
This rule guarantees the lowest average cost among all possible decision strategies.
Real-Time Example: Medical Diagnosis
Imagine a medical test for detecting a rare disease.
- Disease prevalence (prior probability): P(Disease)=0.01
- Test sensitivity: P(Positive∣Disease)=0.9
- Test false positive rate: P(Positive∣NoDisease)=0.05
Bayesian Decision Theory helps calculate P(Disease∣Positive), the posterior probability that a patient has the disease after a positive test.
It also considers losses — the cost of missing a disease vs. the cost of a false alarm — to determine the optimal decision threshold for diagnosis.
Bayesian Decision Theory in Machine Learning
Modern machine learning algorithms heavily rely on Bayesian concepts for prediction, inference, and decision-making.
Applications:
- Naive Bayes Classifier: Assumes independence among features and uses Bayes’ theorem for classification.
- Bayesian Neural Networks: Incorporate uncertainty into model weights.
- Reinforcement Learning: Uses Bayesian priors to improve exploration strategies.
- Gaussian Processes: Use Bayesian inference for non-parametric regression.
Comparing Bayesian and Frequentist Approaches
| Aspect | Bayesian Approach | Frequentist Approach |
| Basis | Probability as belief | Probability as frequency |
| Uses Prior Knowledge | Yes | No |
| Output | Probability distribution | Point estimate |
| Flexibility | High | Moderate |
| Example | Bayesian Decision Theory | Hypothesis testing (t-test, z-test) |
Bayesian methods are more adaptable to uncertainty and dynamic conditions, while frequentist methods excel in fixed, repeatable environments.
Applications in AI and Business Analytics
Bayesian Decision Theory is integral to multiple industries:
a. Finance
- Portfolio optimization
- Credit risk modeling
- Fraud detection
b. Healthcare
- Medical diagnostics
- Clinical trial analysis
- Personalized treatment plans
c. Marketing
- Customer segmentation
- Recommendation systems
- Conversion probability analysis
d. Autonomous Systems
- Self-driving cars
- Robotics decision-making
- Real-time environment adaptation
Bayesian Networks and Their Importance
Bayesian Networks (BNs) are graphical models representing probabilistic relationships between variables.
They help visualize dependencies and support causal reasoning in complex systems.
Example:
A BN for disease prediction may include nodes for symptoms, test results, and disease status, connected via probabilistic links.
Image Suggestion:
- A labeled Bayesian Network diagram
Alt Text: “Bayesian Network showing probabilistic relationships between variables.”
Theoretical Foundation: Decision-Theoretic Bayesian Inference
Bayesian Decision Theory can be generalized as a probabilistic framework for optimal decision-making under uncertainty. The key concept is minimizing expected loss (or maximizing expected utility) rather than relying solely on maximum likelihood estimates.
Mathematically, for a decision rule d(x), the Bayes Risk is defined as:
R(d)=∫R(θ,d)π(θ)dθ
where
- R(θ,d) is the conditional risk for a given parameter θ,
- π(θ) is the prior distribution.
A Bayes decision rule minimizes R(d), leading to the most rational action under probabilistic uncertainty.
This principle can be viewed as an intersection of statistical inference, optimization, and economics, forming the theoretical foundation of modern AI decision systems.
Bayesian Decision Rule in Continuous Spaces
In many real-world cases, decisions are not discrete but continuous. For example, predicting the price of a stock or estimating medical dosage requires continuous decisions.
Here, the loss function could be squared error loss:
L(θ,a)=(θ−a)2
The Bayes action minimizing expected loss is the posterior mean:
a∗=E[θ∣x]
This is a fundamental result used in Bayesian regression, forecasting, and signal estimation.
Types of Loss Functions in Bayesian Decision Theory
Different scenarios use specific loss functions. Choosing an appropriate one is crucial for accurate modeling.
| Type of Loss Function | Mathematical Expression | Use Case |
| 0-1 Loss | L(θ,a)=0 if a=θ;1 otherwise | Classification decisions |
| Quadratic Loss | L(θ,a)=(θ−a)2 | Regression and forecasting |
| Absolute Loss | ( L(\theta, a) = | \theta – a |
| Asymmetric Loss | Different penalties for over/underestimation | Risk management, pricing |
| Logarithmic Loss | ( L(\theta, a) = -\log(P(a | \theta)) ) |
Relationship Between Bayesian Decision Theory and Machine Learning
Modern supervised learning and classification models directly stem from Bayesian Decision Theory principles:
- Naive Bayes Classifier → Applies Bayes’ theorem to compute posterior class probabilities.
- Bayesian Neural Networks (BNNs) → Introduce uncertainty by modeling weights as distributions.
- Gaussian Processes → Use Bayesian inference for continuous predictions.
- Reinforcement Learning → Uses Bayesian updates to balance exploration vs exploitation.
For example, in binary classification:
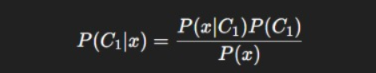
A decision rule is chosen to minimize misclassification loss — typically, assign xxx to the class with the higher posterior probability.
Bayesian Decision Theory in Real-World Applications
Let’s examine real-world case studies where Bayesian Decision Theory is practically applied.
a. Financial Risk Management
Banks use Bayesian decision models to update credit risk based on prior transaction behavior and new evidence.
Example: Predicting loan default probability using prior client data and ongoing repayment behavior.
b. Medical Diagnosis
In healthcare, Bayesian inference is used to combine prior disease prevalence with test results to make optimal diagnostic decisions.
Example: If a disease has 1% prevalence and a test has 95% sensitivity, Bayesian decision theory gives the true posterior probability that the patient is infected.
c. Autonomous Vehicles
Self-driving cars use Bayesian networks to predict pedestrian movement and make real-time driving decisions under uncertainty.
d. Fraud Detection
Bayesian decision models update the likelihood of fraud with every new transaction feature (time, location, amount).
e. Marketing and Recommendation Systems
Posterior probability estimates user interests, guiding targeted ad placements or product recommendations.
Bayesian Decision Theory vs. Frequentist Decision Theory
| Feature | Bayesian | Frequentist |
| Approach | Probabilistic, uses priors | Relies only on data |
| Interpretation | Probability as belief | Probability as frequency |
| Decision Rule | Minimizes expected loss | Based on long-run averages |
| Use Case | Adaptive models, uncertainty quantification | Hypothesis testing |
| Modern Example | Bayesian Optimization | Frequentist Linear Regression |
This difference is crucial in AI systems where new data continuously updates the model’s understanding.
Advanced Mathematical Example
Problem: Suppose we classify emails as spam or not spam.

If the loss for misclassifying spam as not spam is 2x the opposite case, Bayesian decision theory will choose the posterior with minimum expected risk, adjusting the decision threshold accordingly.
Bayesian Decision Networks (BDNs)
BDNs are graphical models that integrate decision nodes, chance nodes, and utility nodes.
They visually represent dependencies and optimal policies.
Applications include:
- Supply chain decision-making
- Clinical treatment planning
- Predictive maintenance in industry
They combine probabilistic reasoning (Bayes networks) with decision analysis for end-to-end optimization.
Bayesian Decision Theory in Deep Learning
- Bayesian Neural Networks (BNNs) assign prior distributions to model weights instead of fixed values.
- This allows uncertainty estimation — critical in fields like healthcare or self-driving systems where decisions under uncertainty can be life-critical.
- Example: A BNN outputs both a mean prediction and a confidence score for tumor classification.
Bayesian Decision Theory in AI Ethics and Policy
As AI systems become autonomous, ethical decision-making under uncertainty (e.g., in healthcare triage or autonomous vehicles) must be optimized.
Bayesian Decision Theory provides the formal foundation for encoding ethical priors, such as:
- minimizing harm,
- balancing false positives/negatives,
- prioritizing fairness across groups.
Advantages and Limitations
Advantages
- Handles uncertainty elegantly.
- Integrates prior knowledge effectively.
- Adaptable to dynamic data streams.
- Provides probabilistic confidence intervals.
Limitations
- Computationally intensive for large models.
- Sensitive to choice of priors.
- Requires domain expertise to define meaningful loss functions.
Future of Bayesian Decision Theory
As data becomes more complex, the importance of Bayesian reasoning grows.
With advancements in probabilistic programming, deep Bayesian learning, and AI ethics, Bayesian Decision Theory is evolving into a core framework for explainable AI.
Emerging trends include:
- Integration with Large Language Models (LLMs) for adaptive reasoning.
- Automated prior learning using meta-learning.
- Hybrid Bayesian-Frequentist models for robust decision-making.
Conclusion
Bayesian Decision Theory is not just a mathematical framework — it’s a philosophy of intelligent decision-making under uncertainty.
By combining probability, data, and cost-sensitive reasoning, it delivers optimal, interpretable, and data-driven solutions for real-world challenges.As machine learning and AI continue to evolve, Bayesian methods will remain at the heart of intelligent, ethical, and explainable systems.
FAQ’s
What is the Bayesian decision theory?
Bayesian Decision Theory is a statistical approach that uses probability and prior knowledge to make optimal decisions under uncertainty by minimizing expected loss or maximizing expected utility.
What are the advantages of Bayesian decision theory?
The advantages of Bayesian Decision Theory include its ability to handle uncertainty effectively, incorporate prior knowledge, update beliefs with new data, and make more accurate and consistent decisions compared to traditional methods.
How can Bayes’ theorem be used in decision making?
Bayes’ theorem is used in decision-making by updating the probability of an event based on new evidence, allowing individuals or systems to make more informed and data-driven choices under uncertainty.
What is an example of a Bayesian decision?
An example of a Bayesian decision is a medical diagnosis, where doctors update the probability of a disease after receiving new test results, helping them choose the most likely and effective treatment.
What is the Bayes decision rule?
The Bayes decision rule is a principle that selects the decision with the lowest expected loss (or highest expected utility) based on the posterior probabilities derived from Bayes’ theorem.