Modern machine learning is not only about predicting outcomes but also about understanding uncertainty. Many real-world problems involve incomplete, noisy, or ambiguous information.
Probabilistic models allow systems to reason under uncertainty. Instead of providing rigid predictions, they quantify likelihoods and confidence levels. This approach is particularly useful in domains such as healthcare, finance, and natural language processing.
Foundations of Bayesian Reasoning
Bayesian reasoning is based on updating beliefs as new evidence becomes available. It follows a simple idea: prior knowledge should be combined with observed data to make informed decisions.
This philosophy contrasts with purely deterministic approaches. Bayesian methods continuously revise predictions as more data arrives.
Understanding Bayes’ Law and Bayes’ Theorem
Bayes’ law, also known as Bayes’ theorem, describes the relationship between conditional probabilities.
It answers a fundamental question:
What is the probability of an event given that another event has occurred?
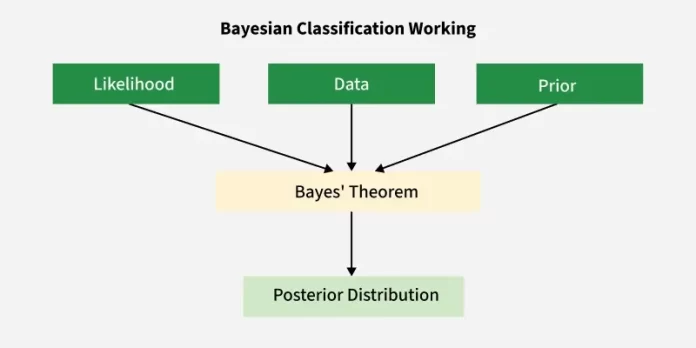
Bayes’ theorem forms the mathematical foundation for all Bayesian classifiers.
The Bayes Equation Explained Simply
The Bayes equation can be expressed conceptually as:
- Probability of hypothesis given evidence
- Proportional to likelihood of evidence given hypothesis
- Multiplied by prior probability of hypothesis
This equation balances prior belief and observed evidence.
What Is a Bayes Classifier
A Bayes classifier is a probabilistic machine learning model that assigns class labels based on Bayes’ theorem. It calculates the probability that a data point belongs to a particular class and chooses the class with the highest probability.
Rather than learning complex decision boundaries, the model relies on probability distributions.
How a Bayes Classifier Works
The workflow follows a structured process:
- Estimate prior probabilities for each class
- Compute likelihood of features given each class
- Apply Bayes’ theorem to compute posterior probabilities
- Assign the class with the highest posterior value
This simplicity makes the model efficient and scalable.
Assumptions Behind Bayesian Classification
Bayesian classifiers make assumptions about data generation.
Common assumptions include:
- Features are conditionally independent
- Data follows known probability distributions
- Prior probabilities are representative
While these assumptions may not always hold, the classifier often performs well in practice.
Types of Bayes Classifiers
Several variants exist depending on feature distribution assumptions.
The most widely used variants include:
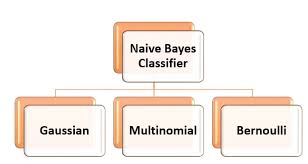
- Naive Bayes
- Gaussian Bayes
- Multinomial Bayes
- Bernoulli Bayes
Each variant suits different data types.
Naive Bayes Classifier Explained
The Naive Bayes classifier assumes that features are independent given the class label.
Despite this strong assumption, it performs surprisingly well in many applications, especially text classification.
Its simplicity leads to fast training and prediction.
Gaussian Bayes Classifier
Gaussian Bayes assumes that continuous features follow a normal distribution.
It is commonly used when features are numeric and continuous, such as sensor readings or financial metrics.
The model estimates mean and variance for each feature per class.
Multinomial Bayes Classifier
Multinomial Bayes is designed for discrete count data.
It is widely used in natural language processing tasks such as document classification and topic modeling.
Word frequencies serve as input features.
Bernoulli Bayes Classifier
Bernoulli Bayes handles binary features.
It focuses on whether a feature is present or absent rather than its frequency.
This variant is useful for binary text representations.
Mathematical Intuition Behind the Model
Bayes classifiers compute posterior probabilities using multiplication of likelihoods and priors.
Logarithmic transformations are often used to prevent numerical underflow and simplify computation.
This mathematical efficiency contributes to the model’s popularity.
Training a Bayes Classifier
Training involves estimating probability distributions from labeled data.
The process includes:
- Counting feature occurrences
- Estimating probabilities
- Applying smoothing techniques
Laplace smoothing is commonly used to handle unseen values.
Bayes Classifier in Probabilistic Modeling
A Bayes classifier is fundamentally a probabilistic model. Instead of learning rigid decision boundaries, it estimates probabilities and makes predictions based on likelihoods.
This probabilistic nature allows the classifier to express uncertainty. Unlike deterministic models, a Bayes classifier can indicate confidence levels for predictions, which is valuable in real-world decision-making.
Probabilistic modeling is especially important in domains such as healthcare, finance, and risk assessment, where uncertainty must be quantified rather than ignored.
Relationship Between Bayes’ Law and Conditional Probability
Bayes’ law is derived from the definition of conditional probability. It mathematically connects prior beliefs with new evidence.
In practical terms:
- Prior probability represents existing knowledge
- Likelihood represents observed evidence
- Posterior probability represents updated belief
This relationship allows a Bayes classifier to continuously improve predictions as more data becomes available.
Prior Probability Selection and Its Impact
The choice of prior probabilities significantly affects model behavior, especially when data is limited.
Types of priors include:
- Uniform priors, assuming equal likelihood
- Empirical priors, based on historical data
- Informative priors, derived from domain expertise
In small datasets, priors can dominate predictions. In large datasets, their influence gradually decreases.
Likelihood Estimation in Bayes Classifiers
Likelihood estimation determines how features relate to class labels.
Common approaches include:
- Gaussian distributions for continuous features
- Multinomial distributions for count-based data
- Bernoulli distributions for binary features
Accurate likelihood estimation improves classification accuracy and robustness.
Bayes Classifier Assumptions and Their Consequences
Most practical implementations rely on simplifying assumptions.
The most common assumption is conditional independence among features. While this assumption is often violated in real data, the classifier still performs well in many scenarios.
Understanding these assumptions helps analysts:
- Interpret results correctly
- Avoid overconfidence
- Choose suitable datasets
Naive Bayes vs Full Bayesian Classifiers
Naive Bayes assumes feature independence, while full Bayesian classifiers model feature dependencies explicitly.
Naive Bayes advantages:
- Computational efficiency
- Scalability
- Simplicity
Full Bayesian models:
- Capture complex relationships
- Require more data and computation
The choice depends on problem complexity and resource availability.
Bayes Classifier in Text Classification
Text data is one of the most successful application areas.
Bayes classifiers are widely used for:
- Spam detection
- Sentiment analysis
- Document categorization
- Email filtering
The probabilistic framework handles high-dimensional feature spaces efficiently, making it suitable for natural language processing tasks.
Real-Time Example: Spam Email Detection
Spam detection illustrates the power of Bayes’ theorem clearly.
The classifier evaluates:
- Probability of spam given certain words
- Probability of legitimate email given the same words
By comparing posterior probabilities, it determines whether an email should be flagged as spam.
This method remains effective even with evolving spam patterns.
Bayes Classifier in Medical Diagnosis
Medical decision systems often rely on Bayesian reasoning.
A Bayes classifier can estimate the probability of a disease given observed symptoms and test results.
Benefits include:
- Transparent reasoning
- Incorporation of prior medical knowledge
- Adaptability to new evidence
This makes Bayesian methods valuable in clinical decision support systems.
Handling Missing Data with Bayes Classifiers
Bayes classifiers handle missing data more gracefully than many algorithms.
Because predictions are based on probability distributions, missing features can be ignored or marginalized without discarding entire records.
This capability is useful in real-world datasets where missing values are common.
Bayes Classifier vs Discriminative Models
Bayes classifiers are generative models, while algorithms like logistic regression and support vector machines are discriminative.
Key differences:
- Generative models learn joint probability distributions
- Discriminative models learn decision boundaries
Generative models offer interpretability, while discriminative models often achieve higher predictive accuracy.
Interpretability and Explainability
Interpretability is a major advantage of Bayes classifiers.
Each prediction can be explained using probabilities, making the decision process transparent. This is critical in regulated industries where explainability is required.
Bayesian models naturally align with explainable AI principles.
Computational Efficiency and Scalability
Bayes classifiers are computationally efficient.
Training involves estimating probabilities rather than optimizing complex objective functions. This allows:
- Fast training
- Low memory usage
- Scalability to large datasets
These properties make them suitable for real-time and embedded systems.
Hybrid Approaches Using Bayes Classifiers
Modern systems often combine Bayesian methods with other models.
Examples include:
- Using Bayes classifiers for feature selection
- Combining Bayesian outputs with neural networks
- Bayesian ensembles for uncertainty estimation
These hybrid approaches leverage the strengths of multiple techniques.
Bayesian Thinking Beyond Classification
Bayesian reasoning extends beyond classification tasks.
Applications include:
- Bayesian regression
- Bayesian optimization
- Bayesian networks
- Probabilistic graphical models
Learning Bayes classifiers provides a foundation for more advanced probabilistic modeling.
Bayes Classifier in Modern Machine Learning Pipelines
Despite advances in deep learning, Bayes classifiers remain relevant.
They are often used:
- As baseline models
- In resource-constrained environments
- For fast prototyping
- When interpretability is critical
Their simplicity and robustness ensure continued adoption.
Ethical Considerations in Bayesian Models
Bayesian models rely on prior knowledge, which can introduce bias.
Ethical considerations include:
- Careful selection of priors
- Regular model evaluation
- Transparency in assumptions
Responsible use ensures fair and unbiased outcomes.
Prediction Process Step by Step
During prediction:
- Input features are extracted
- Likelihoods are calculated
- Posterior probabilities are computed
- Highest probability class is selected
This process is computationally lightweight.
Real-World Example in Email Spam Detection
Email spam filtering is one of the most famous applications.
Words in an email act as features. The classifier calculates how likely an email is spam given the words it contains.
Despite its simplicity, this approach remains effective at scale.
Real-World Example in Medical Diagnosis
In healthcare, Bayes classifiers assist in diagnosis.
Symptoms act as features, while diseases represent class labels. The model combines historical disease prevalence with observed symptoms to estimate probabilities.
This probabilistic reasoning supports clinical decision-making.
Real-World Example in Text Classification
News categorization, sentiment analysis, and document tagging rely heavily on Bayesian models.
Their ability to handle high-dimensional data efficiently makes them ideal for text-heavy tasks.
Bayes Classifier vs Other Machine Learning Algorithms
Compared to decision trees or neural networks, Bayes classifiers are simpler and faster.
They require less training data and are less prone to overfitting in high-dimensional spaces.
However, they may underperform when feature dependencies are strong.
Strengths of Bayesian Classification
Key advantages include:
- Fast training and prediction
- Robust performance with small datasets
- Interpretability
- Scalability
These strengths make them suitable for baseline models.
Limitations of Bayes Classifiers
Despite their strengths, limitations exist.
Common challenges include:
- Strong independence assumptions
- Reduced performance with correlated features
- Limited expressive power
Understanding these limitations ensures proper usage.
Performance Considerations
Bayes classifiers perform best when:
- Features are informative
- Data is well-preprocessed
- Smoothing is applied correctly
Feature engineering plays a critical role.
Feature Engineering for Bayes Models
Effective features improve accuracy.
Best practices include:
- Removing irrelevant features
- Normalizing numeric data
- Handling missing values
- Using appropriate text preprocessing
Well-designed features compensate for model simplicity.
Applications Across Industries
Bayesian classifiers are used in:
- Finance for risk assessment
- Healthcare for diagnosis
- Marketing for customer segmentation
- Cybersecurity for threat detection
Their versatility supports wide adoption.
Visualization and Interpretation
Probabilistic outputs enable transparency.
Visualizing class probabilities helps stakeholders understand model confidence and uncertainty.
Best Practices for Practical Use
Recommended practices include:
- Starting with Naive Bayes as a baseline
- Evaluating assumptions
- Comparing with more complex models
- Monitoring performance over time
This ensures reliable deployment.
Common Mistakes and How to Avoid Them
Typical mistakes include:
- Ignoring data preprocessing
- Misinterpreting probabilities
- Overlooking feature dependence
Careful validation mitigates these risks.
Final Thoughts and Key Takeaways
Bayes classifiers demonstrate that powerful machine learning models do not need complexity. By combining Bayes’ law, prior knowledge, and observed data, these models deliver fast, interpretable, and effective classification solutions.
Understanding their theory and practical application provides a strong foundation for anyone working in machine learning, data science, or artificial intelligence.
FAQ’s
What is Bayesian classification and how does it work?
Bayesian classification is a probabilistic machine learning approach that uses Bayes’ Theorem to predict a class by calculating the probability of outcomes based on prior knowledge and observed data.
What are the three types of naïve Bayes classifiers?
The three types of Naïve Bayes classifiers are Gaussian Naïve Bayes, Multinomial Naïve Bayes, and Bernoulli Naïve Bayes, each suited for different data distributions and use cases.
What is a Bayes classifier in digital image processing?
A Bayes classifier in digital image processing is a probabilistic method that assigns image pixels or features to classes by applying Bayes’ Theorem to minimize classification error based on prior probabilities and likelihoods.
What is the Bayes algorithm used for?
The Bayes algorithm is used for probabilistic classification and prediction, enabling systems to make decisions under uncertainty by updating probabilities based on observed data.
What are the three main types of classifiers?
The three main types of classifiers are binary classifiers, multiclass classifiers, and multilabel classifiers, depending on how many classes or labels they predict.