Sklearn Regression: The Ultimate Power Guide to Mastering Predictive Modeling

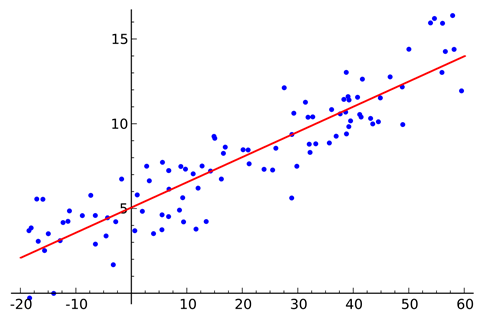
Regression is one of the fundamental concepts in machine learning. It focuses on predicting a continuous numerical outcome based on given input variables. For instance:

• Predicting house prices based on size, location, and features
  
• Estimating medical costs based on patient demographics and health conditions
  
• Forecasting stock prices or sales trends

In the Python ecosystem, regression models are widely implemented using the Scikit-learn (sklearn) library. Known for its simplicity, consistency, and wide range of tools, sklearn regression has become the go-to choice for beginners and professionals alike.

Why Use Sklearn for Regression?

Scikit-learn is one of the most widely adopted machine learning libraries due to:

• Consistency in API design: Easy to learn and use across models
  
• Wide range of regression models: From simple linear regression to advanced ensemble methods
  
• Integration with NumPy, Pandas, and Matplotlib
  
• Preprocessing tools: Scaling, normalization, encoding
  
• Cross-validation utilities for robust model evaluation
  
• Model persistence: Saving and reusing trained models

These features make sklearn regression a reliable and powerful framework for both academic research and enterprise-level projects.

Types of Regression Models in Sklearn

Linear Regression

• Simple yet powerful baseline model.
  
• Equation: y = β0 + β1×1 + β2×2 + … + βnxn
  
• Example: Predicting salary based on years of experience.

Ridge Regression

• Linear regression with L2 regularization.
  
• Prevents overfitting by penalizing large coefficients.

Lasso Regression

• Uses L1 regularization.
  
• Performs feature selection by shrinking less important coefficients to zero.

ElasticNet Regression

• Combination of Ridge and Lasso.
  
• Balances bias and variance effectively.

Polynomial Regression

• Extends linear regression by adding polynomial terms.
  
• Example: Modeling non-linear relationships in growth patterns.

Logistic Regression (for Classification)

• Despite its name, logistic regression is used for classification tasks.
  
• Example: Predicting whether a customer will churn or not.

Decision Tree Regression

• Non-linear model based on tree structures.
  
• Great for interpretability but prone to overfitting.

Random Forest Regression

• An ensemble of decision trees.
  
• More robust and generalizes better than a single tree.

Gradient Boosting Regression

• Sequentially builds trees to minimize error.
  
• Example: Widely used in Kaggle competitions for accuracy.

Support Vector Regression (SVR)

• Uses hyperplanes to fit regression lines.
  
• Works well in high-dimensional spaces.

K-Nearest Neighbors Regression (KNN)

• Predicts value based on closest neighbors.
  
• Simple but computationally expensive on large datasets.

Bayesian Ridge Regression

• Probabilistic model that includes uncertainty in predictions.

Other Advanced Models

• Huber Regression
  
• Quantile Regression
  
• Theil-Sen Estimators

How Sklearn Regression Works Under the Hood

Sklearn regression follows a standard pipeline:

1. Data preprocessing: Handling missing values, scaling, and encoding
   
2. Splitting data: Train-test split or cross-validation
   
3. Model training: Fit method to train regression models
   
4. Prediction: Using the predict() function
   
5. Evaluation: Metrics like R², MAE, RMSE, MSE

This consistency makes it easy to switch between different regression algorithms without changing the overall workflow.

Steps to Implement Regression with Sklearn

• Import libraries: scikit-learn, pandas, numpy
  
• Load dataset (example: housing prices dataset)
  
• Preprocess data (handle null values, scaling)
  
• Train-test split
  
• Train regression model using fit()
  
• Make predictions using predict()
  
• Evaluate performance with metrics like r2_score or mean_squared_error

Real-World Use Cases of Sklearn Regression

• Healthcare: Predicting patient recovery time based on treatments
  
• Finance: Loan default risk estimation
  
• Retail: Forecasting product demand
  
• Manufacturing: Predictive maintenance of machinery
  
• Marketing: Customer lifetime value prediction

Advantages and Limitations of Sklearn Regression

Advantages

• Easy to implement
  
• Wide range of regression algorithms
  
• Integration with data science ecosystem
  
• Strong community and documentation

Limitations

• May struggle with extremely large datasets (need distributed systems like Spark MLlib)
  
• Limited support for deep learning compared to TensorFlow/PyTorch

Comparison with Other Regression Libraries

• TensorFlow/PyTorch: Better for deep learning, but sklearn is simpler for regression tasks
  
• Statsmodels: Great for statistical analysis, but sklearn offers broader ML tools
  
• XGBoost/LightGBM: Specialized for boosting methods, often outperform sklearn’s Gradient Boosting

Best Practices for Using Sklearn Regression

• Always normalize/standardize data for models like SVR or KNN
  
• Use cross-validation to avoid overfitting
  
• Regularization techniques (Lasso, Ridge) for high-dimensional data
  
• Feature engineering to improve predictive performance
  
• Hyperparameter tuning using GridSearchCV or RandomizedSearchCV

Hands-on Example with Python Code

import pandas as pd

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from sklearn.metrics import r2_score, mean_squared_error

# Sample dataset

data = pd.read_csv("housing.csv")

X = data[["size", "bedrooms", "age"]]

y = data["price"]

# Train-test split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Train model

model = LinearRegression()

model.fit(X_train, y_train)

# Predictions

y_pred = model.predict(X_test)

# Evaluation

print("R2 Score:", r2_score(y_test, y_pred))

print("MSE:", mean_squared_error(y_test, y_pred))

Advanced Regression Metrics Beyond R² and MSE

Most tutorials stop at R², MSE, or RMSE. However, advanced practitioners often use additional metrics:

• Mean Absolute Percentage Error (MAPE): Useful in forecasting, gives error as a percentage.
  
• Median Absolute Error (MedAE): Robust against outliers.
  
• Explained Variance Score: Measures variance explained by the model predictions.
  
• Adjusted R²: Accounts for the number of features in the model, penalizing overfitting.

Example:

from sklearn.metrics import mean_absolute_percentage_error, median_absolute_error, explained_variance_score

mape = mean_absolute_percentage_error(y_test, y_pred)

medae = median_absolute_error(y_test, y_pred)

evs = explained_variance_score(y_test, y_pred)

print("MAPE:", mape)

print("Median Absolute Error:", medae)

print("Explained Variance:", evs)

Feature Selection and Engineering in Sklearn Regression

Regression performance often hinges on feature quality.

• VarianceThreshold: Removes low-variance features.
  
• Recursive Feature Elimination (RFE): Iteratively selects best predictors.
  
• L1-based feature selection (Lasso): Zeroes out irrelevant features.
  
• PolynomialFeatures: Captures non-linear relationships.

Example:

from sklearn.feature_selection import RFE

from sklearn.linear_model import LinearRegression

model = LinearRegression()

selector = RFE(model, n_features_to_select=3)

selector = selector.fit(X_train, y_train)

print("Selected Features:", selector.support_)

Hyperparameter Tuning for Regression Models

Many regression models require careful tuning. Sklearn provides:

• GridSearchCV: Exhaustive search over specified parameter values.
  
• RandomizedSearchCV: Random combinations, faster for large search spaces.
  
• Bayesian Optimization (via skopt): More efficient tuning for complex models.

Example (Ridge Regression tuning):

from sklearn.linear_model import Ridge

from sklearn.model_selection import GridSearchCV

params = {'alpha': [0.01, 0.1, 1, 10, 100]}

ridge = Ridge()

grid = GridSearchCV(ridge, params, cv=5, scoring='r2')

grid.fit(X_train, y_train)

print("Best Alpha:", grid.best_params_)

Regularization Techniques in Depth

Regularization is crucial for avoiding overfitting:

• Ridge (L2): Penalizes large coefficients, but keeps all features.
  
• Lasso (L1): Shrinks some coefficients to zero, performs feature selection.
  
• ElasticNet: Combines both.

Advanced insight:

• Ridge is preferred when many small/medium effects are expected.
  
• Lasso is ideal when only a few features drive predictions.
  
• ElasticNet is useful when correlations exist among predictors.

Scaling and Normalization for Regression Models

Some models (SVR, KNN, Lasso) are sensitive to scale. Sklearn preprocessing offers:

• StandardScaler: Mean=0, Std=1
  
• MinMaxScaler: Values scaled between 0 and 1
  
• RobustScaler: Ignores outliers by using median and IQR

Example:

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

X_scaled = scaler.fit_transform(X)

Cross-Validation Techniques for Regression

Instead of a single train-test split, advanced practitioners use:

• K-Fold Cross-Validation: Dataset split into k parts
  
• Leave-One-Out (LOO): Each observation becomes a test set once
  
• Repeated K-Fold: Multiple iterations of K-fold
  
• Time Series Split: For sequential data like stock prices

Example:

from sklearn.model_selection import cross_val_score

scores = cross_val_score(model, X, y, cv=10, scoring='r2')

print("Cross-Validation R² Scores:", scores)

Pipelines in Sklearn Regression

Pipelines streamline workflow by chaining preprocessing and modeling steps.

Example:

from sklearn.pipeline import Pipeline

from sklearn.preprocessing import StandardScaler

from sklearn.linear_model import Lasso

pipeline = Pipeline([

    ('scaler', StandardScaler()),

    ('lasso', Lasso(alpha=0.1))

])

pipeline.fit(X_train, y_train)

Benefits:

• Prevents data leakage
  
• Ensures reproducibility
  
• Simplifies model deployment

Regression with Imbalanced Data

When target values are skewed (e.g., predicting rare expensive house prices), strategies include:

• Log-transform target variable
  
• Quantile regression for handling skewness
  
• SMOTE for regression (SMOGN) in rare regression cases

Model Interpretability in Sklearn Regression

Advanced regression requires interpretability, especially in finance and healthcare:

• Permutation Importance: Measures feature contribution
  
• Partial Dependence Plots (PDPs): Shows effect of one feature on predictions
  
• SHAP Values: Explain predictions at feature level

Example:

from sklearn.inspection import permutation_importance

results = permutation_importance(model, X_test, y_test, scoring='r2')

print(results.importances_mean)

Ensemble Regression Techniques

Ensembles combine models for stronger predictions:

• Bagging Regressor: Trains multiple base regressors and averages results
  
• Stacking Regressor: Combines multiple models with a meta-model
  
• Voting Regressor: Simple average of multiple regressors

Example:

from sklearn.ensemble import StackingRegressor

from sklearn.linear_model import RidgeCV

from sklearn.svm import SVR

estimators = [

    ('ridge', RidgeCV()),

    ('svr', SVR(kernel='linear'))

]

stacking = StackingRegressor(estimators=estimators, final_estimator=RidgeCV())

stacking.fit(X_train, y_train)

Regression on High-Dimensional Data

For datasets with thousands of features:

• Use PCA (Principal Component Analysis) before regression
  
• Apply Lasso or ElasticNet for feature selection
  
• Employ dimensionality reduction with feature importance ranking

Time Series Regression with Sklearn

Though sklearn is not specialized for time series, regression can still be applied:

• Use lag features (previous values as predictors)
  
• Add rolling averages, trends, and seasonal features
  
• Combine with TimeSeriesSplit for validation

Sklearn Regression in Production

Steps to deploy regression models:

1. Train and validate model
   
2. Save using joblib or pickle
   
3. Deploy as API (Flask, FastAPI, Django)
   
4. Monitor performance drift

Example:

import joblib

joblib.dump(model, "regression_model.pkl")

Integrating Sklearn Regression with Other Tools

• Pandas & Numpy: Data preprocessing
  
• Matplotlib & Seaborn: Visualization
  
• TensorFlow/PyTorch: Hybrid deep learning + sklearn workflows
  
• MLflow: Tracking experiments

Case Study: Sklearn Regression in Business

Scenario: Predicting Used Car Prices

• Dataset: Car features (mileage, year, brand, engine size)
  
• Model: Random Forest Regressor
  
• Outcome: Predicted resale value with RMSE < 1000

Business Impact:

• Car dealerships used regression models to optimize pricing strategies, leading to 12% higher profit margins.

Latest Research Trends in Regression

• Explainable AI (XAI) for regression interpretability
  
• Automated Regression Pipelines with AutoML (TPOT, Auto-Sklearn)
  
• Hybrid Regression Models combining traditional ML with neural networks
  
• Uncertainty Estimation in regression (probabilistic models)

Common Mistakes to Avoid

• Ignoring feature scaling in models like SVR and KNN
  
• Using all features without checking multicollinearity
  
• Not tuning hyperparameters
  
• Relying solely on R² score instead of using multiple metrics

Future of Regression in Machine Learning

• Increasing use of automated machine learning (AutoML) for regression
  
• Integration with big data platforms like Spark
  
• Hybrid models combining regression with deep learning for better accuracy
  
• Explainable regression models for compliance in healthcare and finance

Conclusion

Sklearn regression remains one of the most effective tools for predictive modeling in data science. From simple linear models to advanced ensemble methods, it provides flexibility, consistency, and ease of use. By combining real-world datasets with proper preprocessing, hyperparameter tuning, and evaluation, practitioners can build robust models that drive meaningful insights and business value.

If you are just starting out with regression or looking to optimize your existing models, sklearn regression offers everything you need to build, test, and deploy predictive systems effectively.

FAQ’s