Mastering Confusion Matrix Jacobian: A Powerful Guide for Smarter Machine Learning

When evaluating the performance of a machine learning classification model, the Confusion Matrix is one of the most powerful tools for visualizing predictions. But when combined with Jacobian matrices, it becomes a strong analytical framework for understanding model sensitivity, optimization, and feature influence.

In this guide, we will break down how the Confusion Matrix Jacobian works, why it matters, and how you can use it to make smarter decisions in machine learning projects.

What is the Confusion Matrix?

A Confusion Matrix is a 2×2 (or multi-class) table used to evaluate the performance of a classification model by comparing predicted labels with actual labels.
Instead of giving one number (accuracy), it breaks down model performance into correctly and incorrectly classified instances, making it one of the most insightful tools in machine learning evaluation.

Metrics Based on Confusion Matrix Data

The confusion matrix forms the foundation for many essential classification metrics:

1. Accuracy

Accuracy=TP+TN / TP+FP+FN+TN​

Measures overall correctness—but fails under class imbalance.

2. Precision

Precision=TP / TP+FP​

Measures how many predicted positives were actually correct.

3. Recall (Sensitivity)

Recall=TP / TP+FN​

Shows how many actual positives the model successfully detected.

4. Specificity

Specificity=TN / TN+FP​

Important for detecting false alarms.

5. F1 Score

F1=2×Precision⋅Recall / Precision+Recall​

Balances precision and recall.

6. False Positive Rate

FPR=FP / FP+TN​

7. False Negative Rate

FNR=FN / TP+FN​

8. ROC & AUC Metrics

Derived from FP and TP rates for threshold-based evaluation.

These metrics give a complete understanding of a model’s strengths and weaknesses.

The Confusion Matrix Structure

For a binary classification model, the confusion matrix looks like this:

Actual \ Predicted	Positive	Negative
Positive	TP	FN
Negative	FP	TN

Explanation of cells:

• TP (True Positive): Correctly predicted positive cases
  
• TN (True Negative): Correctly predicted negative cases
  
• FP (False Positive): Incorrectly predicted positive (Type I Error)
  
• FN (False Negative): Incorrectly predicted negative (Type II Error)

For multi-class problems, this becomes an N × N matrix where each row is the actual class and each column is the predicted class.

Confusion Matrix Terminology

These terms appear frequently in ML evaluation:

True Positive (TP)

Actual = Positive, Predicted = Positive
Correct detection of the event.

False Positive (FP)

Actual = Negative, Predicted = Positive
Model raises an unnecessary alarm.

False Negative (FN)

Actual = Positive, Predicted = Negative
Model misses an important case.

True Negative (TN)

Actual = Negative, Predicted = Negative
Correct rejection of non-events.

Type I Error

FP — the model falsely identifies something as positive.

Type II Error

FN — the model fails to detect a true positive.

Support

Number of actual occurrences of each class.

These fundamentals form the basis of advanced evaluation using Jacobians.

Why Confusion Matrix is Essential in Machine Learning

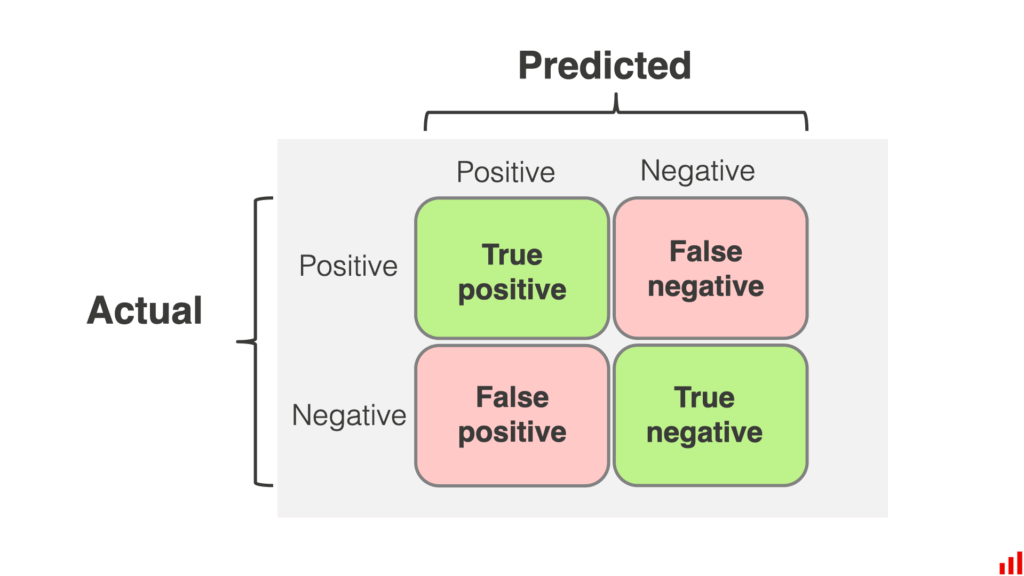
A confusion matrix provides a detailed breakdown of True Positives (TP), True Negatives (TN), False Positives (FP), and False Negatives (FN), helping us:

• Measure accuracy beyond a single percentage score.
  
• Identify class imbalance problems.
  
• Understand the trade-off between precision and recall.
  

For example:
If your spam email classifier labels 95% of emails as non-spam correctly but fails at detecting 20% of spam emails, this can lead to real-world security issues.

Understanding the Jacobian in Mathematics and ML

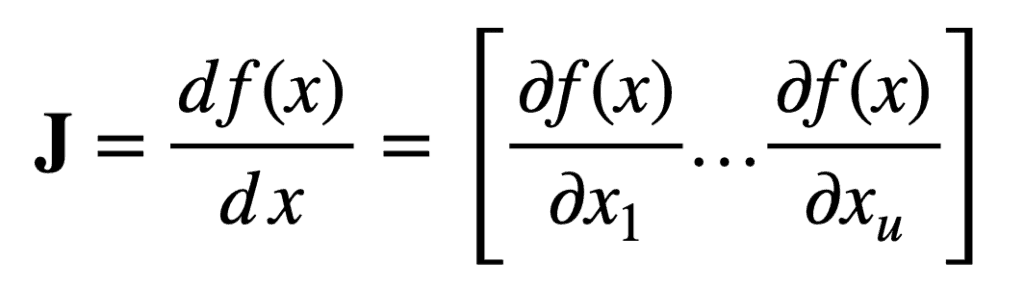
The Jacobian is a matrix of all first-order partial derivatives of a vector-valued function. In machine learning, it is crucial for:

• Measuring sensitivity of model output with respect to input parameters.
  
• Gradient-based optimization in deep learning.
  
• Stability analysis in control systems.

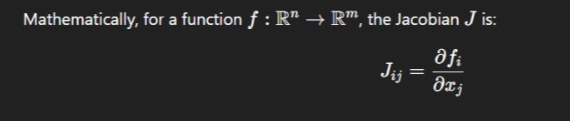
Confusion Matrix Jacobian: Bridging Evaluation and Optimization

When we talk about the Confusion Matrix Jacobian, we refer to calculating the rate of change in confusion matrix values with respect to input parameters or model hyperparameters.

Benefits:

• Optimization: Fine-tuning model thresholds for better F1 scores.
  
• Sensitivity Analysis: Understanding how changes in feature importance affect classification performance.
  

Key Components of a Confusion Matrix

Prediction \ Actual	Positive	Negative
Positive	TP	FP
Negative	FN	TN

• True Positives (TP): Correctly predicted positives.
  
• True Negatives (TN): Correctly predicted negatives.
  
• False Positives (FP): Incorrectly predicted positives.
  
• False Negatives (FN): Missed positives.
  

Mathematical Representation of the Jacobian in Classification Model

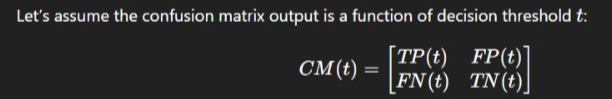
Jacobian with respect to ttt will show how small changes in the threshold affect TP, FP, FN, and TN.

Real-Time Example: Spam Email Classification

Imagine you’re building a spam filter using logistic regression:

• At threshold t=0.5t = 0.5t=0.5, you get TP = 80, FP = 10, FN = 20, TN = 90.
  
• If you adjust ttt slightly, the confusion matrix changes.
  
• The Jacobian tells you how sensitive each value is to threshold changes.
  

This helps you balance recall and precision depending on business needs.

Step-by-Step: Computing the Confusion Matrix Jacobian in Python

import numpy as np
from sklearn.metrics import confusion_matrix
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

# Example dataset

X = np.random.rand(200, 4)
y = np.random.randint(0, 2, 200)

# Train model

model = LogisticRegression()
model.fit(X, y)
probs = model.predict_proba(X)[:, 1]

# Function to compute confusion matrix at a given threshold

def cm_at_threshold(threshold):
 preds = (probs >= threshold).astype(int)
return np.array(confusion_matrix(y, preds))

# Numerical approximation of the Jacobian

threshold = 0.5
delta = 0.01
J = (cm_at_threshold(threshold + delta) - cm_at_threshold(threshold - delta)) / (2 * delta)
print("Jacobian of Confusion Matrix:\n", J)

Visualizing the Confusion Matrix Jacobian

Definition Link – Combines the confusion matrix (model performance evaluation) with the Jacobian matrix (sensitivity of outputs to parameter changes).

Purpose – Shows how small changes in model parameters affect each cell of the confusion matrix (TP, TN, FP, FN).

Visualization Method – Commonly uses heatmaps to highlight magnitude and direction of change for each metric.

Insights – Helps identify which parameters most influence accuracy, precision, recall, or other classification metrics.

Trade-off Detection – Reveals areas where improving one metric (e.g., recall) may worsen another (e.g., specificity).

Advanced Use – Can integrate dimensionality reduction (PCA, t-SNE) for high-dimensional models and enable interactive exploration for parameter tuning.

Including visual aids helps interpret results:

• Heatmaps to show confusion matrix values.
  
• Surface plots for Jacobian sensitivity across thresholds.
  

Common Pitfalls and How to Avoid Them

• Overfitting to metrics: Don’t optimize just for accuracy; consider F1 score.
  
• Ignoring class imbalance: Always balance datasets before training.
  
• Misinterpreting Jacobian values: Sensitivity ≠ importance.

The Role of a Confusion Matrix

The Confusion Matrix plays a central role in machine learning because it:

1. Provides granular information

Shows exactly where the model is failing (FP or FN).

2. Helps analyze class imbalance

Accuracy alone hides imbalance — confusion matrices make it visible.

3. Supports metric calculations

Precision, recall, specificity, F1, AUC — all derived from confusion matrix values.

4. Helps business decision-making

Industries prioritize metrics differently:

• Healthcare → reduce FN (missed disease)
  
• Finance → reduce FP (false fraud alerts)
  
• Security → balance FP and FN

5. Assists in threshold tuning

By tracking how TP, FP, FN, and TN change with thresholds.

Limitations of Accuracy as a Standalone Metric

Accuracy alone can be highly misleading.

1. Fails under Imbalanced Datasets

Example: Fraud detection
If 99% are legitimate and model predicts “legit” always:
Accuracy = 99% but model is useless.

2. Doesn’t show error direction

Whether model:

• mistakes positives as negatives (FN)
  
• mistakes negatives as positives (FP)

Matters a LOT in sensitive use cases.

3. Cannot inform thresholds

Accuracy does not change meaningfully when decision thresholds shift.

4. Not suitable for multi-class imbalance

Some classes may be ignored but accuracy can still remain high.

This is why confusion matrices are essential.

The Benefits of a Confusion Matrix

A confusion matrix offers benefits far beyond accuracy:

1. Complete performance breakdown

Explains classification errors in detail.

2. Supports custom metric optimization

Businesses can optimize:

• Recall (healthcare)
  
• Precision (e-commerce)
  
• Specificity (fraud detection)

3. Enables threshold tuning

By analyzing how TP/FP/FN/TN change with thresholds.

4. Visualization clarity

Heatmaps clearly show which classes perform poorly.

5. Foundation for advanced sensitivity analysis

When combined with Jacobians, it reveals how metrics change with respect to:

• Feature variations
  
• Threshold adjustments
  
• Hyperparameter tuning

This bridges evaluation with optimization.

Calculating a Confusion Matrix

The confusion matrix is simple to compute using Python.

Python Example

from sklearn.metrics import confusion_matrix

# true labels

y_true = [1, 0, 1, 1, 0, 0]

# predicted labels

y_pred = [1, 0, 0, 1, 0, 1]

cm = confusion_matrix(y_true, y_pred)

print(cm)

Output

[[2 1]

 [1 2]]

This corresponds to:

• TN = 2
  
• FP = 1
  
• FN = 1
  
• TP = 2

Step-by-Step Manual Calculation

1. For each sample, compare predicted vs actual.
   
2. Increase respective cell:
   
   • If actual = 1 and predicted = 1 → TP++
     
   • If actual = 0 and predicted = 1 → FP++
     
   • If actual = 1 and predicted = 0 → FN++
     
   • If actual = 0 and predicted = 0 → TN++

For multi-class models

Use:

confusion_matrix(y_true, y_pred, labels=[0,1,2,3])

Real-World Applications Across Industries

• Healthcare: Detecting disease with optimized sensitivity.
  
• Finance: Fraud detection models tuned for minimal false negatives.
  
• Manufacturing: Predictive maintenance with minimal downtime misclassifications.
  

External Tools and Resources

• Scikit-learn Confusion Matrix Documentation
  
• NumPy Gradient & Jacobian
  
• Purpose – External tools and resources supplement in-house capabilities by providing specialized functions, datasets, or visualization options.
  
• Data Analysis Tools – Platforms like Excel, Tableau, or Power BI help in exploring and presenting results more effectively.
  
• Machine Learning Libraries – Frameworks such as scikit-learn, TensorFlow, or PyTorch offer pre-built methods for computing confusion matrices and Jacobians.
  
• Visualization Utilities – Tools like Matplotlib, Seaborn, or Plotly allow creation of detailed and interactive performance plots.
  
• Learning Platforms – Websites like Analytics Vidhya, Kaggle, or Coursera provide tutorials, datasets, and case studies to deepen understanding.
  
• laboration Tools – GitHub, Google Colab, and Jupyter Notebooks enable sharing code, experiments, and analysis with peers.

Conclusion and Best Practices

Combining the Confusion Matrix with the Jacobian gives ML practitioners a deeper, sensitivity-aware evaluation tool. This ensures models aren’t just accurate, but also robust and adaptable to real-world changes.

FAQ’s