Understanding the Geometry Behind Gaussian Curvature in Mathematics and Data Science

Modern data science relies heavily on probabilistic thinking. Whether the problem involves geometry, signal processing, clustering, or regression, Gaussian-based methods appear repeatedly because of their mathematical elegance and practical reliability.

Across disciplines such as differential geometry, statistics, and machine learning, Gaussian formulations provide smoothness, uncertainty estimation, and analytical tractability. This article explores how these ideas connect, culminating in Gaussian Process Regression, a flexible and powerful modeling framework used in modern analytics.

Rather than treating each concept in isolation, this blog builds a logical bridge from foundational mathematics to applied machine learning.

Mathematical Foundations of Gaussian Concepts

The Gaussian function forms the backbone of many mathematical and statistical models. It is defined by its smooth bell-shaped curve and governed by mean and variance.

Key properties include:

• Symmetry around the mean
• Rapid decay toward infinity
• Closed-form integration in multidimensional spaces
• Stability under linear transformations

These properties make Gaussian functions ideal for modeling natural phenomena and uncertainty.

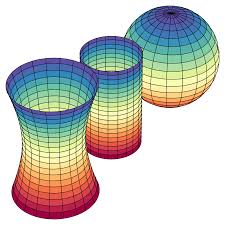
Understanding Gaussian Curvature in Geometry

Gaussian curvature originates in differential geometry and measures how a surface bends at a point.

Unlike mean curvature, Gaussian curvature depends solely on intrinsic properties of a surface.

Key insights:

• Positive curvature indicates sphere-like shapes
• Zero curvature corresponds to flat surfaces
• Negative curvature appears in saddle-shaped surfaces

Real-world relevance includes:

• Surface reconstruction in computer graphics
• Shape analysis in medical imaging
• Terrain modeling in geospatial analysis

Although geometric, Gaussian curvature introduces the idea of local structure, which later becomes essential in kernel-based learning models.

Gaussian Functions and Their Integration

A Gaussian function is defined as:

• Smooth
• Infinitely differentiable
• Parameterized by mean and variance

Gaussian function integration plays a crucial role in probability theory and machine learning.

Applications include:

• Normalization of probability density functions
• Bayesian inference
• Kernel density estimation

In practice, Gaussian integration allows models to compute expectations and marginal probabilities efficiently.

The Gaussian Integral and Why It Matters

The Gaussian integral is one of the most important results in mathematics because it has a closed-form solution despite involving an exponential quadratic term.

Why it matters:

• Enables normalization of probability distributions
• Forms the backbone of Bayesian statistics
• Allows analytical solutions in Gaussian processes

Without the Gaussian integral, probabilistic machine learning would rely far more heavily on numerical approximations.

From Probability to Learning: Gaussian Distributions

Gaussian distributions dominate statistical modeling because of:

• Central Limit Theorem implications
• Noise modeling capabilities
• Analytical convenience

In machine learning, Gaussian assumptions appear in:

• Linear regression residuals
• Hidden Markov models
• Bayesian networks

These assumptions naturally extend into mixture models and process-based learning.

Gaussian Mixture Model Explained

A Gaussian Mixture Model represents data as a combination of multiple Gaussian distributions.

Key characteristics:

• Soft clustering rather than hard assignments
• Probabilistic membership
• Flexible modeling of complex distributions

Each component captures a different underlying data structure.

Gaussian Mixture Models in Real-World Data

Gaussian mixture models are widely used in:

• Customer segmentation
• Image segmentation
• Speech recognition
• Anomaly detection

Example:

In finance, transaction data often contains overlapping spending behaviors. Gaussian mixture models separate these behaviors probabilistically instead of forcing rigid clusters.

Introduction to Gaussian Processes

A Gaussian process is a collection of random variables where any finite subset follows a multivariate Gaussian distribution.

Unlike parametric models:

• No fixed equation is assumed
• The model adapts based on data
• Uncertainty is explicitly quantified

Gaussian processes are defined by:

• Mean function
• Covariance function (kernel)

Gaussian Process Regression Deep Dive

Gaussian Process Regression models functions directly instead of estimating parameters.

Key advantages:

• Provides predictive uncertainty
• Works well with small datasets
• Highly flexible non-linear modeling

This approach is particularly useful in scientific modeling where understanding uncertainty is as important as prediction accuracy.

Kernel Functions and Covariance Structure

The kernel defines similarity between data points.

Common kernels include:

• Radial Basis Function
• Matérn kernel
• Rational quadratic kernel

Choosing the right kernel allows Gaussian Process Regression to model periodicity, smoothness, and noise effectively.

Mathematical Intuition Behind Gaussian-Based Models

Gaussian-based methods are favored not only because of convenience but because they reflect how uncertainty propagates in real systems. When independent random effects accumulate, their combined behavior converges toward a Gaussian distribution. This explains why Gaussian assumptions appear repeatedly in physics, economics, and machine learning.

In regression problems, uncertainty is rarely uniform. Gaussian Process Regression models this non-uniform uncertainty explicitly by allowing variance to change across the input space. This capability makes it superior for domains where confidence estimation matters as much as accuracy.

Relationship Between Gaussian Integrals and Probabilistic Inference

Gaussian integrals allow closed-form solutions for marginal likelihoods and posterior distributions. This is especially important in Bayesian learning frameworks.

In Gaussian Process Regression:

• Posterior predictions rely on multivariate Gaussian integrals
  
• Marginal likelihood optimization uses Gaussian integral properties
  
• Hyperparameter tuning becomes analytically tractable
  

Without Gaussian integrals, inference would require heavy numerical approximation, significantly increasing computational cost and reducing model reliability.

Why Gaussian Mixture Models Complement Gaussian Processes

Although Gaussian Mixture Models and Gaussian Process Regression solve different problems, they are often used together in real-world pipelines.

Examples include:

• Using Gaussian Mixture Models to cluster time series, followed by Gaussian Process Regression per cluster
  
• Modeling multimodal input distributions before applying regression
  
• Noise modeling using mixture components
  

This hybrid approach improves robustness when data exhibits multiple underlying patterns.

Uncertainty Quantification as a Competitive Advantage

One of the strongest benefits of Gaussian Process Regression is its built-in uncertainty estimation. Instead of producing a single prediction, the model outputs a distribution.

Practical advantages include:

• Risk-aware decision making
  
• Confidence-driven automation
  
• Early anomaly detection
  

Industries such as finance, healthcare, and autonomous systems increasingly prioritize models that explain uncertainty, not just predictions.

Scalability Improvements in Modern Gaussian Process Implementations

Historically, Gaussian Process Regression struggled with scalability due to cubic time complexity. Modern techniques now mitigate this issue.

Key advancements include:

• Sparse Gaussian Processes
  
• Inducing point approximations
  
• Variational inference methods
  
• Kernel interpolation techniques
  

These approaches allow Gaussian Process Regression to scale to tens or even hundreds of thousands of data points in production systems.

Interpretability Compared to Deep Learning Models

While deep learning models often outperform in raw predictive power, they lack transparency. Gaussian Process Regression provides:

• Explicit covariance structure
  
• Explainable kernel behavior
  
• Interpretable uncertainty intervals
  

This makes it a preferred choice in regulated industries where explainability is mandatory.

Choosing the Right Kernel for Real-World Data

Kernel selection defines model behavior. Poor kernel choice can lead to underfitting or excessive smoothness.

General guidance:

• Use RBF kernels for smooth continuous data
  
• Use Matérn kernels for rough or noisy signals
  
• Combine kernels to capture periodic trends and long-term structure
  

Kernel composition allows Gaussian Process Regression to model complex real-world patterns without increasing model opacity.

Role of Gaussian Processes in Modern Analytics Pipelines

In modern data pipelines, Gaussian Process Regression often appears in:

• Forecasting systems
  
• Optimization loops
  
• Simulation models
  
• Digital twin architectures
  

Its ability to update predictions dynamically as new data arrives makes it ideal for real-time analytics environments.

Ethical and Responsible Modeling Considerations

Uncertainty-aware models reduce overconfidence, which is a major source of algorithmic harm. Gaussian Process Regression naturally discourages extrapolation beyond observed data, making it safer for deployment in sensitive domains.

Responsible benefits include:

• Transparent uncertainty communication
  
• Reduced false confidence
  
• Better human-in-the-loop decision support
  

Historical Evolution of Gaussian-Based Methods

Gaussian concepts have evolved over centuries, beginning with Carl Friedrich Gauss’s work on error analysis. Initially applied to astronomy and physics, Gaussian distributions later became foundational in probability theory. As computing advanced, these ideas transitioned from pure mathematics into machine learning and statistical modeling.

Gaussian Mixture Models emerged as a solution to represent real-world data that could not be captured by a single normal distribution. Gaussian Process Regression later extended these ideas by modeling entire functions probabilistically rather than estimating fixed parameters.

This historical progression shows how Gaussian theory naturally adapts to increasingly complex data-driven problems.

Mathematical Stability and Numerical Advantages

Gaussian-based models exhibit strong numerical stability compared to many alternative probabilistic approaches. This stability arises from:

• Well-conditioned covariance matrices
  
• Closed-form likelihood expressions
  
• Smooth optimization landscapes
  

These properties reduce convergence failures and make Gaussian methods reliable in production systems where numerical errors can lead to costly failures.

Gaussian Curvature Beyond Geometry

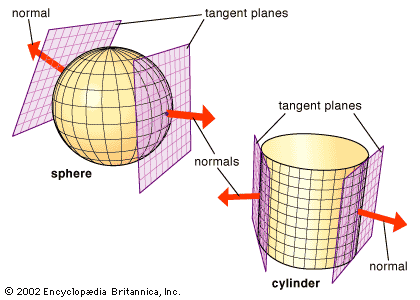
While Gaussian curvature originates in differential geometry, its conceptual interpretation extends to data surfaces. In machine learning, curvature can be interpreted as how rapidly model behavior changes across the feature space.

High curvature regions often correspond to:

• Decision boundaries
  
• Rapid variance changes
  
• Anomalous data regions
  

Understanding curvature helps practitioners identify unstable regions in learned models and improve robustness.

Practical Comparison with Parametric Models

Unlike parametric models that assume a fixed functional form, Gaussian Process Regression adapts its structure based on data. This makes it especially useful when:

• The underlying relationship is unknown
  
• Data availability is limited
  
• Flexibility is required without overfitting
  

Parametric models may converge faster, but Gaussian Process Regression offers superior adaptability when uncertainty and structure are unknown.

Handling Noise with Gaussian Mixture Models

Real-world datasets often contain heterogeneous noise sources. Gaussian Mixture Models are uniquely suited for this challenge by allowing different components to represent different noise patterns.

Use cases include:

• Sensor fusion systems
  
• Financial volatility modeling
  
• Image segmentation with varying illumination
  

This ability to separate structured signals from noise improves downstream modeling accuracy.

Role in Bayesian Optimization

Gaussian Process Regression serves as the backbone of Bayesian optimization techniques. By modeling the objective function probabilistically, it allows:

• Efficient exploration of unknown spaces
  
• Reduced evaluation cost
  
• Intelligent trade-offs between exploration and exploitation
  

This is widely used in hyperparameter tuning, materials science, and experimental design.

Interpretability Through Covariance Structure

Unlike black-box models, Gaussian-based methods expose relationships directly through covariance matrices. These matrices reveal:

• Feature similarity
  
• Correlation strength
  
• Spatial or temporal dependencies
  

This transparency allows domain experts to validate model behavior against real-world knowledge.

Integration with Deep Learning Systems

Modern hybrid systems combine Gaussian processes with neural networks. Examples include:

• Deep kernel learning
  
• Gaussian process layers in neural networks
  
• Bayesian neural networks with Gaussian priors
  

These hybrid approaches retain uncertainty estimation while scaling to large datasets.

Real-World Deployment Challenges and Solutions

Although powerful, Gaussian-based models require careful implementation. Common challenges include:

• Memory constraints for large covariance matrices
  
• Kernel mis-specification
  
• Overconfidence in sparse regions
  

Solutions include sparse approximations, kernel learning techniques, and uncertainty-aware deployment strategies.

Industry-Specific Impact

Gaussian methods are heavily adopted across industries:

• Healthcare: Disease progression modeling
  
• Finance: Risk estimation and portfolio optimization
  
• Manufacturing: Predictive maintenance
  
• Climate Science: Environmental forecasting
  

Their probabilistic nature aligns well with real-world uncertainty.

Future Directions of Gaussian-Based Modeling

Research continues to enhance Gaussian frameworks through:

• Scalable variational inference
  
• Non-stationary kernel learning
  
• Integration with reinforcement learning
  
• Automated kernel discovery
  

These advancements ensure Gaussian-based methods remain relevant in next-generation analytics systems.

Real-World Applications of Gaussian Process Regression

Gaussian Process Regression is widely used in:

• Time-series forecasting
• Hyperparameter optimization
• Robotics control systems
• Climate modeling
• Medical diagnosis

Example:

In predictive maintenance, Gaussian Process Regression estimates failure probabilities while quantifying uncertainty in sensor readings.

Comparison with Other Regression Models

Compared to linear regression:

• Captures non-linear patterns
• Provides uncertainty intervals

Compared to neural networks:

• Requires less data
• More interpretable uncertainty
• Higher computational cost for large datasets

Practical Challenges and Scalability

Limitations include:

• Computational complexity
• Memory usage with large datasets

Solutions involve:

• Sparse Gaussian processes
• Approximate inference
• Inducing point methods

Visual Interpretation and Model Intuition

Gaussian Process Regression produces:

• Mean prediction curve
• Confidence intervals

This visualization improves trust and interpretability, especially in high-stakes decision-making environments.

Conclusion

Gaussian-based methods form a unified mathematical framework connecting geometry, probability, and machine learning. From Gaussian curvature describing surface behavior to Gaussian integrals enabling probabilistic reasoning, these concepts converge naturally in Gaussian Process Regression.

By modeling uncertainty directly and adapting flexibly to data, Gaussian Process Regression stands as one of the most powerful tools for modern analytics. Understanding its mathematical roots not only improves implementation but also deepens trust in predictive systems built on probabilistic foundations.

FAQ’s