In a world driven by data, making accurate predictions is more important than ever. Whether you’re analyzing business trends, forecasting sales, or identifying patterns in scientific research, a regression model is your go-to statistical tool. At the heart of this technique lies the regression line, a visual representation of how variables relate and interact.
If you’re looking to improve decision-making through data, learning how to build and interpret regression models is a must-have skill—get started today and unlock actionable insights from your data.
What is a Regression Model?
Defining the Tool of Prediction
A regression model is a statistical method used to examine the relationship between one dependent variable and one or more independent variables. It helps us understand how changes in the independent variable(s) affect the dependent variable, allowing for prediction and inference.
Basic Equation of Linear Regression:

Y=a+bX+εY = a + bX + \varepsilon
Where:
- Y = Dependent variable
- X = Independent variable
- a = Intercept (value of Y when X is 0)
- b = Slope (change in Y for each unit change in X)
- ε = Error term
This simple equation forms the foundation of linear regression, the most commonly used regression model.
The Role of the Regression Line
A Visual Guide to Relationships
The regression line represents the best fit through a scatter plot of data points. It minimizes the distance (or error) between the observed values and the values predicted by the model.
Why It Matters:
- Shows the trend: The line clearly illustrates whether there’s a positive, negative, or no relationship.
- Predicts values: You can estimate unknown outcomes for new inputs.
- Identifies outliers: Points far from the line signal unusual behavior or noise.
Types of Regression Models
1. Simple Linear Regression
- Involves one independent and one dependent variable.
- Example: Predicting house price (Y) based on square footage (X).
2. Multiple Linear Regression
- Uses two or more independent variables to predict the dependent variable.
- Example: Predicting sales using advertising spend, number of salespeople, and store location.
3. Polynomial Regression
- Uses higher-degree terms (e.g., X², X³) to capture non-linear relationships.
- Example: Predicting growth rates that accelerate or decelerate over time.
4. Logistic Regression (Though not a “regression line” in the traditional sense)
- Used for binary outcomes (yes/no, true/false).
- Example: Predicting whether a customer will buy a product (1) or not (0).
How to Build a Regression Model

Step 1: Collect and Prepare Data
Clean and preprocess your dataset, ensuring variables are relevant and properly formatted.
Step 2: Choose the Right Model
Decide whether a simple, multiple, or polynomial regression fits your data.
Step 3: Fit the Model
Use statistical software like Python (Scikit-learn, Statsmodels), R, or Excel to run the regression.
Step 4: Analyze the Regression Line and Coefficients
Check:
- R-squared: Measures how well the regression line fits the data.
- P-values: Test the significance of each variable.
- Residuals: Ensure errors are randomly distributed.
Step 5: Validate and Predict
Use testing data or cross-validation to ensure accuracy, then apply the model for forecasting or decision-making.
Applications of Regression Models
- Business: Forecasting sales, pricing optimization, and budgeting.
- Healthcare: Predicting patient outcomes or treatment effects.
- Finance: Modeling stock prices or credit risk.
- Education: Estimating student performance based on study hours, attendance, etc.
- Marketing: Understanding customer behavior based on ad exposure and demographics.
How Regression Works
At its core, regression analysis works by finding the mathematical relationship that best describes how a dependent variable (Y) changes in response to one or more independent variables (X). The process involves minimizing the sum of squared errors (SSE) — the differences between observed and predicted values.
In simple terms, regression finds the “line of best fit” through your data, ensuring predictions are as close as possible to actual outcomes.
Step-by-Step Breakdown:
- Data Visualization – Start by plotting the data points on a scatter plot to visually inspect relationships between variables.
- Model Estimation – The regression algorithm calculates coefficients (a and b) that minimize error terms using methods like Ordinary Least Squares (OLS).
- Line of Best Fit – This line represents predicted values (Ŷ = a + bX), where a is the intercept and b is the slope.
- Residual Calculation – The residual (ε = Y – Ŷ) measures how far each observation deviates from the predicted value.
- Model Validation – Goodness-of-fit metrics like R², Adjusted R², and Root Mean Squared Error (RMSE) assess how well the regression model explains variation in the data.
In essence, regression quantifies cause-and-effect relationships, helping analysts move from descriptive to predictive insights.
Regression and Econometrics
Econometrics is the application of regression models to economic data — combining statistical techniques, mathematics, and economic theory to test hypotheses and forecast trends.
In econometrics, regression models are not just about correlation but causation — identifying how one variable truly influences another, accounting for real-world complexities like time, policy, and behavior.
Common Econometric Regression Models:
- Simple Linear Regression: Measures the relationship between two economic indicators (e.g., inflation vs. unemployment).
- Multiple Regression: Examines the effect of several economic variables (e.g., GDP growth predicted by interest rate, investment, and exports).
- Panel Regression Models (Fixed/Random Effects): Used when analyzing data over time across multiple entities (countries, companies, or households).
- Time Series Regression: Helps forecast variables like stock prices, inflation, or exchange rates using lagged data.
Econometric Example:
A central bank economist may use regression to predict GDP growth based on interest rates and consumer spending.
Equation:
GDPt=β0+β1(InterestRatet)+β2(Consumptiont)+εt
By analyzing coefficients (β₁, β₂), economists understand how strongly interest rates or consumption drive GDP — critical for policy decisions.
Calculating Regression
The most common way to calculate a linear regression model is using the Least Squares Method — minimizing the total squared differences between observed (Y) and predicted (Ŷ) values.
Formula for Regression Coefficients:
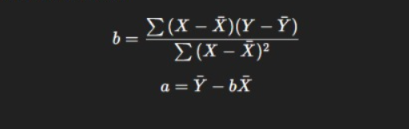
Where:
- b = slope (rate of change of Y with respect to X)
- a = intercept (predicted value of Y when X = 0)
Once the line is calculated, you can use it to predict outcomes for new X values.
Example Calculation:
If you have data showing how marketing spend (X) affects sales (Y):
- Mean(X) = 10, Mean(Y) = 200
- Slope (b) = 15
- Intercept (a) = 50
Equation:
Y=50+15XY = 50 + 15XY=50+15X
So, for a marketing spend of 12, predicted sales = 50 + (15 × 12) = 230.
This predictive capability makes regression invaluable for forecasting and optimization tasks.
Example of Regression Analysis in Finance
Regression analysis plays a vital role in financial modeling, risk management, and investment strategy.
Example 1: Predicting Stock Returns
Analysts use Capital Asset Pricing Model (CAPM) — a regression-based model — to estimate expected stock returns.
Ri=Rf+βi(Rm−Rf)
Where:
- R_i = expected return of the stock
- R_f = risk-free rate
- R_m = market return
- β_i = regression coefficient (beta), representing sensitivity of the stock to market movement
If β = 1.5, the stock is 50% more volatile than the market.
Example 2: Portfolio Optimization
Financial managers use multiple regression to analyze how asset returns depend on various economic factors (interest rates, inflation, or GDP). This helps in constructing portfolios that balance risk and return.
Example 3: Credit Risk Modeling
Banks apply logistic regression to predict the probability of loan default based on borrower characteristics (income, debt ratio, credit score).
These regression-driven insights allow for better financial forecasting, risk management, and investment strategy formulation.
How Is Regression Analysis Used?
Regression analysis has a wide range of applications across industries and academic domains:
1. Business & Marketing
- Forecasting demand and sales trends.
- Determining the impact of advertising spend on revenue.
- Analyzing customer satisfaction drivers.
2. Economics & Finance
- Modeling GDP, inflation, and exchange rate dynamics.
- Estimating asset pricing models and risk exposure.
3. Healthcare & Life Sciences
- Predicting patient recovery times or disease likelihood.
- Assessing treatment effectiveness using clinical data.
4. Education & Social Sciences
- Understanding how factors like attendance, study hours, and parental education affect student performance.
5. Engineering & Technology
- Modeling system performance or predicting equipment failure rates.
Regression analysis turns raw data into actionable intelligence, guiding evidence-based decisions across research, business, and policy.
Advanced Regression Types for Modern Analytics
a. Quantile Regression
Instead of predicting the mean of Y, it predicts specific quantiles (e.g., 25th, 50th, 75th percentiles).
Useful for risk modeling (e.g., predicting Value at Risk in finance) and inequality studies (e.g., income distribution).
b. Robust Regression
Minimizes the effect of outliers by giving them lower weights — valuable when data contains anomalies or measurement errors.
c. Nonlinear Regression
Used when relationships can’t be captured by a straight line.
Example: Growth models, demand curves, or biochemical reaction rates.
d. Bayesian Regression
Integrates prior beliefs (priors) with observed data using probability theory.
Used in predictive modeling under uncertainty, such as forecasting rare events or modeling consumer behavior with limited data.
Integrating Regression with Machine Learning
Modern data science blends traditional regression with machine learning algorithms for superior performance and interpretability.
a. Regression Trees & Random Forests
These non-parametric models handle nonlinear relationships and interactions automatically — ideal for high-dimensional or noisy data.
b. Gradient Boosting Regression (XGBoost, LightGBM, CatBoost)
Sequentially builds strong models by correcting previous errors.
Outperforms traditional regression in complex tasks like financial forecasting and marketing analytics.
c. Neural Network Regression
Deep learning regression models (using TensorFlow or PyTorch) handle large-scale data with complex nonlinearities — from predicting housing prices to energy consumption.
d. Explainable AI (XAI) in Regression
Techniques like SHAP (SHapley Additive exPlanations) or LIME quantify how each feature influences the prediction — the modern counterpart to regression coefficients in interpretable ML.
Regression in Time Series and Forecasting
Regression can be extended to time-dependent data, integrating lagged variables, trends, and seasonality.
a. Autoregressive Distributed Lag (ARDL) Models
Capture both short-term and long-term effects between variables.
b. Regression with ARIMA Residuals
Combines regression with ARIMA models to handle autocorrelation — powerful for forecasting macroeconomic indicators.
c. Vector Autoregression (VAR)**
Used in econometrics to model interdependencies among multiple time series (e.g., inflation, GDP, interest rates).
From Statistical Insight to Business Intelligence
In modern organizations, regression outputs are directly integrated into dashboards and decision systems through tools like:
- Python Dash, Power BI, Tableau – for real-time regression dashboards.
- SQL-based ETL pipelines – to refresh model outputs automatically.
- APIs and MLOps frameworks – to deploy regression models into production environments.
This makes regression not just an academic concept, but a core part of intelligent automation and decision-making ecosystems.
Common Challenges in Regression Analysis
- Multicollinearity: When independent variables are highly correlated with each other, skewing results.
- Overfitting: A model that fits the training data too well but fails on new data.
- Heteroscedasticity: Unequal variance in errors across the data range.
- Non-linearity: When data relationships are not linear but a linear model is applied.
Tip: Always visualize the regression line to ensure your model captures the actual pattern in the data.
Conclusion
The regression model remains one of the most valuable tools in data science, allowing us to explore relationships, test hypotheses, and make predictions with clarity. The regression line not only guides analysis visually but also empowers confident decision-making based on real data patterns.
Ready to harness the power of regression modeling? Start building your own regression models today to make smarter, data-driven decisions across any field you work in.
FAQ’s
How to predict using a regression line?
To predict using a regression line, plug the input (independent variable) value into the regression equation y=a+bx to calculate the predicted output (dependent variable) based on the model’s slope and intercept.
What is precision in regression?
In regression, precision refers to how consistently and accurately the model’s predictions align with actual values, often measured using metrics like RMSE, MAE, or R² to assess the closeness of predicted outcomes to real data.
What are the 7 steps in regression analysis?
The 7 steps in regression analysis are:
Define the Problem – Identify the objective and dependent/independent variables.
Collect Data – Gather relevant, high-quality data for analysis.
Prepare and Clean Data – Handle missing values, outliers, and ensure consistency.
Select the Regression Model – Choose an appropriate type (linear, multiple, logistic, etc.).
Fit the Model – Use statistical or machine learning tools to train the model.
Evaluate the Model – Assess accuracy using metrics like R², RMSE, or MAE.
Interpret and Apply Results – Use insights from the model to make predictions and guide decisions.
What is a regression prediction?
A regression prediction is the estimated value of a dependent variable generated by a regression model based on given input (independent) variables, helping forecast continuous outcomes like sales, prices, or trends.
How to understand a regression line?
A regression line represents the best-fit line through data points that shows the relationship between independent and dependent variables — helping you understand how changes in one variable are associated with changes in the other.



