Heap Data Structure: The Ultimate Guide to Efficient Priority Management

In the world of data structures, efficiency plays a vital role. While arrays and linked lists help us store information, some problems demand priority-based processing. Imagine managing multiple tasks where each has different urgency — how do we ensure the most critical one is handled first?

That’s where the Heap Data Structure comes in. Used heavily in priority queues, graph algorithms, and real-time systems, heaps are fundamental for computer scientists, data engineers, and software developers.

In this guide, we will explore Heap Data Structure in depth — from properties and operations to real-world applications and advanced variants.

What is a Heap Data Structure?

A Heap Data Structure is a specialized binary tree-based structure that satisfies the heap property.

Heap Property

• In a Min Heap, the parent node is always smaller than its child nodes.
  
• In a Max Heap, the parent node is always greater than its child nodes.

Unlike binary search trees (BSTs), heaps are not ordered, but they are complete trees — meaning all levels are filled except possibly the last, which is filled from left to right.

Example:
If we insert [10, 20, 5, 6, 1, 8, 9] into a Min Heap, the structure ensures that the smallest element (1) is always at the root.

Properties of Heap Data Structure

• Completeness: Always a complete binary tree.
  
• Heap Order Property: Parent is either greater or smaller depending on heap type.
  
• Efficient Access: Minimum/maximum element can be accessed in O(1).
  
• Insertion and Deletion: Both can be done in O(log n).
  
• Not a BST: Does not follow left < root < right property.

Types of Heaps

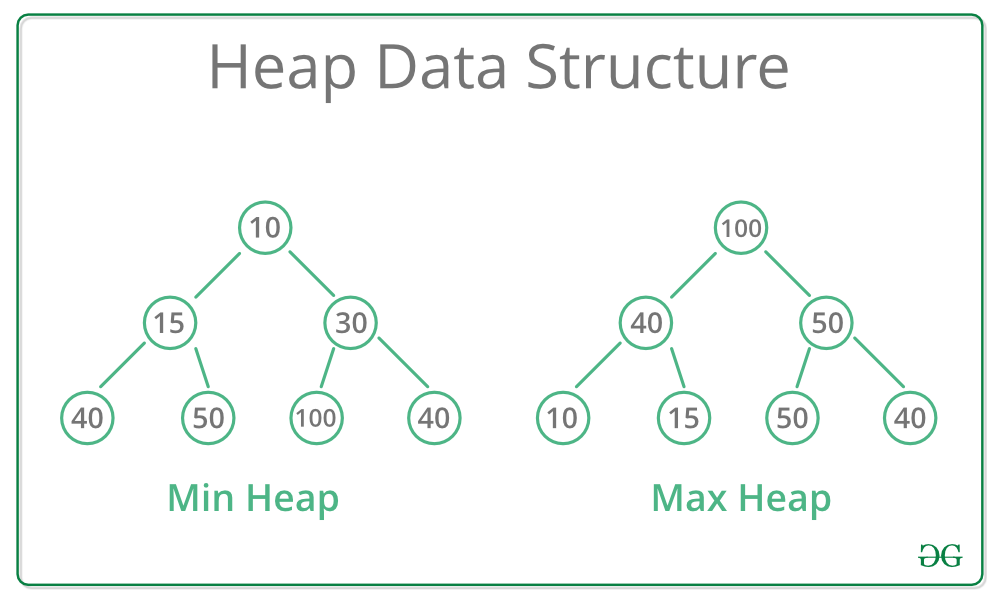
Min Heap

• Root is the minimum element.
  
• Every parent node is smaller than its children.
  
• Useful for implementing priority queues.

Max Heap

• Root is the maximum element.
  
• Every parent node is greater than its children.
  
• Useful in scheduling problems and heap sort.

Binary Heap

• Most common heap structure.
  
• Implemented using arrays.

Fibonacci Heap

• A more advanced heap with better amortized time complexities.
  
• Used in graph algorithms like Dijkstra’s.

Binomial Heap

• Collection of binomial trees.
  
• Efficient for merging heaps.

Why Use Heap Data Structure?

• Efficient implementation of priority queues.
  
• Faster shortest path and minimum spanning tree algorithms.
  
• Great for real-time event simulation.
  
• Supports optimal sorting (heap sort).

Core Operations on Heap

Insertion

• Add element at the end.
  
• Perform heapify up to restore property.

Deletion

• Remove root node (min or max).
  
• Replace with last node and heapify down.

Heapify

• Adjusts elements to maintain heap property.

Extract-Min / Extract-Max

• Removes root element.

Peek

• Returns root without removal.

Example in Python (Min Heap)

import heapq

heap = []

heapq.heappush(heap, 10)

heapq.heappush(heap, 1)

heapq.heappush(heap, 20)

print("Min Element:", heap[0])  # Output: 1

Heap Representation in Memory

• Stored as an array.
  
• Root is at index 0.
  
• For any node at index i:
  
  • Left child = 2i + 1
    
  • Right child = 2i + 2
    
  • Parent = (i-1) // 2

Real-Time Applications of Heap Data Structure

Priority Queues

Operating systems use heaps to schedule processes.

Graph Algorithms

• Dijkstra’s Shortest Path
  
• Prim’s Minimum Spanning Tree

Job Scheduling

Cloud systems use heaps for task prioritization.

Event Simulation

Discrete event simulators use heaps to process events in order.

Data Compression

Huffman coding uses heaps for building optimal prefix codes.

Load Balancing

Heap helps assign tasks to servers efficiently.

Heap Data Structure vs Other Data Structures

Feature	Heap	Stack	Queue	BST
Access Priority	✅	❌	❌	❌
Sorting Support	✅	❌	❌	✅
Balanced Tree	✅	❌	❌	Depends

Implementation of Heap

Python Example:

import heapq

heap = [10, 30, 20]

heapq.heapify(heap)

print("Heap:", heap)  # Min Heap structure

C++ Example:

#include <iostream>

#include <queue>

using namespace std;

int main() {

    priority_queue<int> maxHeap;

    maxHeap.push(10);

    maxHeap.push(20);

    maxHeap.push(5);

    cout << "Max Element: " << maxHeap.top(); // 20

}

Heap Sort Algorithm Explained

• Build max heap.
  
• Swap root with last element.
  
• Heapify reduced heap.
  
• Repeat until sorted.

Time and Space Complexity

Operation	Time Complexity	Space Complexity
Insertion	O(log n)	O(1)
Deletion	O(log n)	O(1)
Peek	O(1)	O(1)
Heapify	O(log n)	O(1)

Advanced Variants of Heaps

• Fibonacci Heap – Better for graph algorithms.
  
• Binomial Heap – Merging heaps efficiently.
  
• Pairing Heap – Simple and efficient in practice.

Advantages and Limitations

Advantages:

• Efficient priority management.
  
• Good for real-time systems.
  
• Useful for graph algorithms.

Limitations:

• Not suitable for searching arbitrary elements.
  
• More overhead compared to arrays for simple tasks.

Real-Time Example: Heap in Operating Systems

Modern OS schedulers use heaps to manage process execution. The process with highest priority (or shortest time) is picked first.

Common Mistakes and Best Practices

• Forgetting to heapify.
  
• Confusing heap with BST.
  
• Using heap for wrong use-cases (like searching).

Lazy vs. Eager Heap Construction

There are two strategies to build heaps:

• Eager Heap Construction: Insert elements one by one into a heap. Complexity → O(n log n).
  
• Lazy Heap Construction (Heapify method): Convert an array into a heap in O(n) using bottom-up heapify.

Advanced insight: The lazy method is why heap sort is efficient for large datasets.

Amortized Analysis in Heap Variants

In traditional Binary Heap, insert and delete take O(log n).
But in Fibonacci Heap, operations achieve:

• Insert → O(1) amortized
  
• Decrease-Key → O(1) amortized
  
• Delete → O(log n)

That’s why Fibonacci Heap is used in graph algorithms (Dijkstra’s & Prim’s) for large-scale networks.

Pairing Heaps – Practical Alternative to Fibonacci

While Fibonacci heaps are theoretically faster, in practical systems, Pairing Heaps often outperform due to their simpler implementation.

• Insert: O(1)
  
• Delete Min: O(log n)
  
• Decrease Key: O(log n) amortized

Real-world: Used in network routing and event simulation systems.

Soft Heaps – Allowing Controlled Errors

A Soft Heap is a variant of heap that allows some errors in priority (corrupts keys slightly) in exchange for faster operations.

• Insert: O(1) amortized
  
• Delete Min: O(log n)
  
• Applications: Approximation algorithms in computational geometry.

Parallel & Distributed Heaps

In Big Data systems, single-thread heaps are inefficient.
Advanced approaches:

• Binomial Heap in Distributed Systems → used for load balancing.
  
• Multi-Queue Heaps → used in parallel processing environments.
  
• Lock-Free Concurrent Heaps → allow multiple threads to perform heap operations without race conditions.

Example: Apache Hadoop’s job scheduler uses multi-level heaps to allocate resources in distributed clusters.

Cache-Efficient Heaps

Modern processors are limited not just by computation, but by cache access.

• Binary Heap can cause cache misses.
  
• Cache-Oblivious Heaps and Van Emde Boas Layout Heaps reduce memory latency.
  
• Used in real-time systems where memory access is critical (like OS schedulers).

External Memory Heaps

When data doesn’t fit into RAM (Big Data / AI training datasets), we need External Memory Heaps.

• Designed to minimize disk I/O operations.
  
• Often used in databases and search engines (e.g., Google indexing).

Heap Augmentation in AI & ML

Heaps are integrated in:

• Feature Selection → selecting top-k features.
  
• K-nearest Neighbors (KNN) → heaps help maintain the nearest distances efficiently.
  
• Deep Learning Frameworks → task queues often use heap-based schedulers.

Example: In TensorFlow, internal operations queue tasks using priority heaps.

Heap in Blockchain & Cryptocurrency

• Transaction Priority Management: Bitcoin & Ethereum miners use heap-based priority queues to pick transactions with higher fees first.
  
• Consensus Algorithms: Some implementations of PBFT (Practical Byzantine Fault Tolerance) use heap scheduling to reduce delays.

Beyond Heap Sort – Hybrid Algorithms

Heap Sort is O(n log n) but often slower in practice compared to QuickSort.
Advanced Hybrid: IntroSort (used in C++ STL sort), starts with QuickSort, switches to Heap Sort if recursion depth grows too large.

This prevents QuickSort’s O(n²) worst-case.

Mathematical Analysis of Heap Height

• A heap of n elements has height log₂n.
  
• Insertion/Deletion complexity directly depends on this height.
  
• In d-ary Heaps (where each node has d children instead of 2):
  
  • Height = logd(n) (shorter trees, fewer levels).
    
  • Used in network packet schedulers.

Heaps in Real-Time AI Systems

Example: Autonomous Cars

• Heaps are used in sensor fusion algorithms to pick top-priority events.
  
• Ensures real-time decisions (like braking) happen without delay.

Example: Financial Trading Systems

• Stock exchanges maintain heaps to quickly match buy/sell orders based on highest/lowest price.

Heap Visualizations & Debugging Tools

For developers, advanced tools like:

• Graphviz Heap Visualizer
  
• HeapView Debugging in Java
  
• Python’s heapq tracing modules

These make heap debugging & optimization easier in real-world systems.

Heap vs. Balanced Trees (AVL, Red-Black)

While AVL Trees and Red-Black Trees maintain strict balance, heaps only maintain the heap property.

• Heap Advantage: Faster array-based representation (better memory locality).
  
• Tree Advantage: Efficient support for searching.
  If you need fast top-k extraction, heaps win. If you need ordered traversal, trees win.

Example: Databases combine both — heaps for priority queues and B-Trees for indexing.

Persistent Heaps

Persistent data structures keep previous versions available after updates.

• Persistent Heaps allow you to maintain multiple states of a heap (useful in undo operations or version control systems).
  
• Used in time-travel queries and blockchain ledgers where historical states must remain accessible.

Heaps in Compiler Design

Compilers and interpreters often use heaps for:

• Dynamic memory allocation (Heap Memory).
  
• Garbage collection → priority heaps help in selecting which memory blocks to free first.
  
• Example: JVM (Java Virtual Machine) uses heap memory management for object storage.

Heap in Operating Systems

• Process Scheduling: OS uses heaps to determine which process runs next (based on priority).
  
• Paging and Virtual Memory: Heaps assist in maintaining least recently used (LRU) structures.
  
• I/O Scheduling: Disk schedulers may use heaps to minimize seek time.

Randomized Heaps (Treaps)

A Treap combines:

• Binary Search Tree (order property).
  
• Heap (priority property).

Treaps are randomized but achieve good expected performance.

• Widely used in computational geometry and randomized algorithms.

Skew Heaps – Self-Adjusting Heaps

• Skew heaps don’t maintain strict structure like binary heaps.
  
• They are self-adjusting, making merges fast.
  
• Used in network packet routing where priorities change dynamically.

Heaps in Real-Time Event Processing

• Game Engines → event-driven updates (AI movement, collisions).
  
• Simulation Systems → event priority handling in large-scale simulations.
  
  Example: NASA uses priority heaps in simulation frameworks for spacecraft trajectory prediction.

Memory-Efficient Heaps (Succinct Heaps)

• Succinct Heaps store heap data in compressed formats.
  
• Reduce memory overhead → useful in embedded systems and IoT devices.
  
  Example: TinyOS (used in sensor networks) integrates memory-efficient heap implementations.

Heap Cryptography & Security Applications

• Priority Queues in Encryption: Used for Huffman Coding (lossless compression).
  
• Zero-Knowledge Proof Systems: Heap variants are being explored in cryptographic data structures.
  
• Blockchain projects research heap-friendly cryptographic accumulators.

Multi-Heaps (Double-Ended Priority Queues)

• A Double-Ended Heap (Deap) supports extracting both min and max efficiently.
  
• Applications:
  
  • Stock trading (highest bid, lowest ask).
    
  • Scheduling with dual constraints (earliest & latest deadlines).

Adaptive Heaps (AI-Driven)

Imagine heaps that learn access patterns and restructure dynamically:

• Machine Learning-enhanced Heaps optimize for predicted workloads.
  
• Could revolutionize cloud computing task scheduling where workloads vary.

Heap in Cloud & Big Data Ecosystems

• Apache Spark & Hadoop use heap-based priority queues for job scheduling.
  
• AWS Auto Scaling → resource allocation decisions often use heap-structured priority evaluators.
  
• Google Borg & Kubernetes → pod scheduling leverages heap priority selection.

Theoretical Research Frontiers

• Quantum Heaps: Future heap models designed for quantum computing task scheduling.
  
• Approximation Heaps: Structures where correctness can be slightly relaxed for speed.
  
• Energy-Aware Heaps: Optimized for low-power AI systems.

Future of Heap in Big Data & AI

With AI and Big Data, heaps are used in:

• Real-time analytics.
  
• Distributed computing.
  
• Large-scale scheduling (Hadoop, Spark).

Conclusion

The Heap Data Structure is a powerful tool in computer science. From priority queues to graph algorithms and real-time applications, heaps remain one of the most versatile structures.By mastering heaps, you gain the ability to optimize algorithms, speed up computation, and design efficient systems.