Cross Validation: The Ultimate Power Guide to Reliable Model Evaluation

Model evaluation is one of the most crucial steps in machine learning. Building a model is not enough; understanding how well it will generalize to unseen data is the real test of success. That’s where cross validation comes in.

Cross validation is a powerful technique to assess the performance of a model and ensure that it isn’t just memorizing the training data but learning patterns that can generalize. In this blog, we’ll explore cross validation in depth, its types, advantages, limitations, practical examples, and implementation in Python using scikit-learn.

What is Cross Validation?

Cross validation is a statistical method used to evaluate machine learning models by splitting the dataset into multiple parts. The goal is to test the model’s ability to generalize to an independent dataset.

Instead of relying on a single train-test split, cross validation provides a more robust way of measuring performance. It does this by dividing data into several folds and training/testing across different subsets.

Why Cross Validation is Important in Machine Learning

When building machine learning models, it’s easy to fall into the trap of overfitting. Overfitting happens when a model performs exceptionally well on training data but poorly on new, unseen data.

Cross validation helps to:

• Provide a reliable estimate of model accuracy.
  
• Reduce bias in performance evaluation.
  
• Avoid overfitting and underfitting.
  
• Support hyperparameter tuning.
  
• Ensure model robustness across different data distributions.

For example, in healthcare, a model predicting patient risk must be validated rigorously using cross validation to ensure it works across different hospitals and patient groups.

Mathematical Foundations of Cross Validation

• Bias-Variance Tradeoff: Explain how cross validation reduces bias in performance estimation while controlling variance.
  
• Generalization Error Bounds: Discuss the relationship between CV results and PAC-learning or Hoeffding’s inequality.

Variants of Cross Validation Beyond Basics

• Repeated k-Fold Cross Validation: Performing k-fold multiple times with different random splits to stabilize results.
  
• Monte Carlo Cross Validation (Shuffle-Split CV): Repeated random splits into train-test sets for high variance scenarios.
  
• Blocked Cross Validation: Specifically for time-series, where folds respect chronological order.
  
• Nested Cross Validation: Used for hyperparameter tuning inside the inner loop and unbiased model evaluation in the outer loop.

Cross Validation in High-Dimensional Data

• p >> n Problem: When features >> samples (e.g., genomics), discuss why leave-one-out CV may lead to overfitting.
  
• Dimensionality Reduction + CV: Show how PCA or feature selection should be done inside the CV loop to avoid data leakage.
  
• Sparse CV: Techniques for handling sparse matrices, especially in NLP with bag-of-words.

Cross Validation in Imbalanced Datasets

• Stratified k-Fold: Ensure each fold respects class distribution for classification.
  
• Weighted Metrics: Why accuracy is misleading and metrics like F1-score, AUC-ROC, PR-AUC must be evaluated within CV.
  
• Resampling Inside CV: Applying SMOTE or undersampling inside training folds, not before splitting.

Cross Validation in Time-Series & Sequential Data

• Rolling Origin / Walk-Forward Validation: Train on past, test on future windows.
  
• Expanding Window CV: Training set grows as time moves forward.
  
• Blocked CV with Gap: Prevents information leakage in autocorrelated data by leaving a gap between train/test splits.                                               

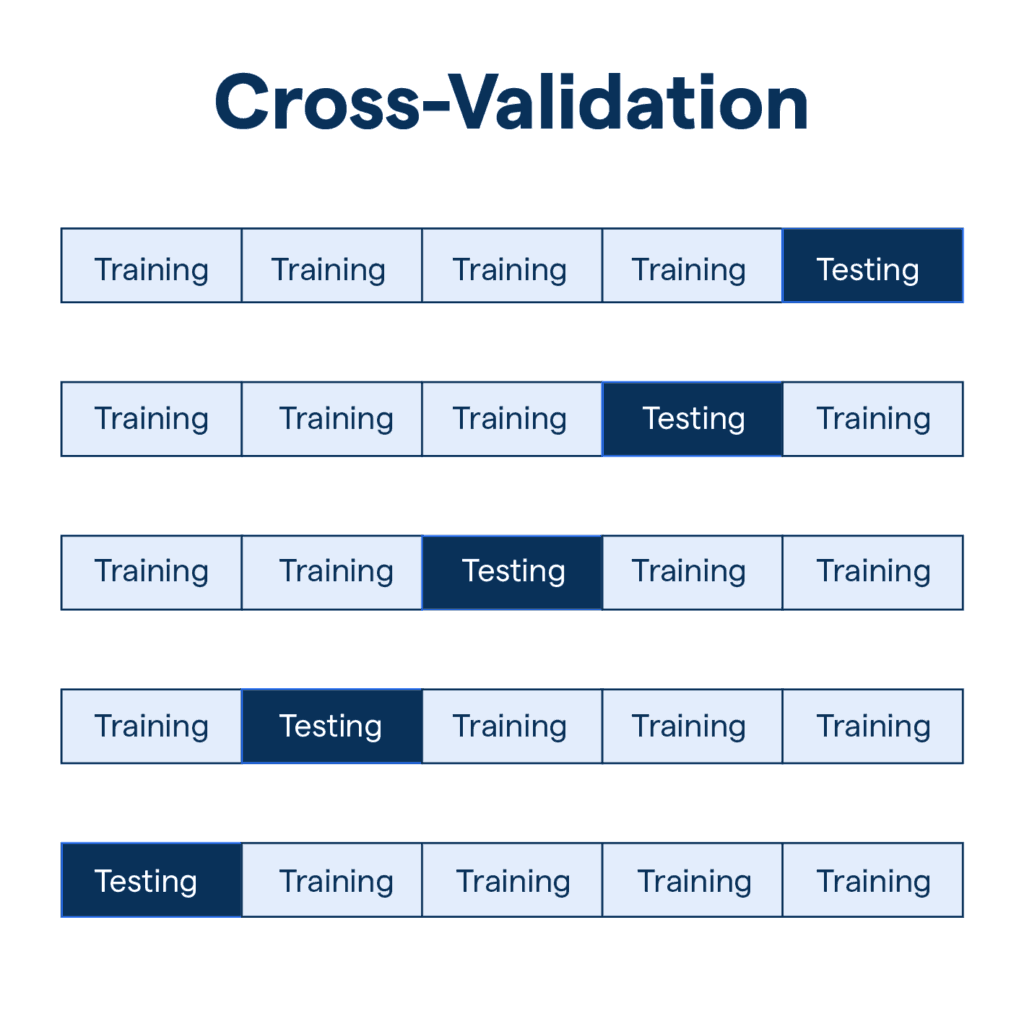
How Cross Validation Works: The Core Idea

At its core, cross validation works by:

1. Splitting the dataset into multiple subsets (folds).
   
2. Training the model on some folds.
   
3. Testing the model on the remaining fold.
   
4. Repeating the process until each fold has been used as a test set.
   
5. Averaging the performance results.

This ensures that every observation in the dataset has been used both for training and testing, giving a reliable performance metric.

Types of Cross Validation

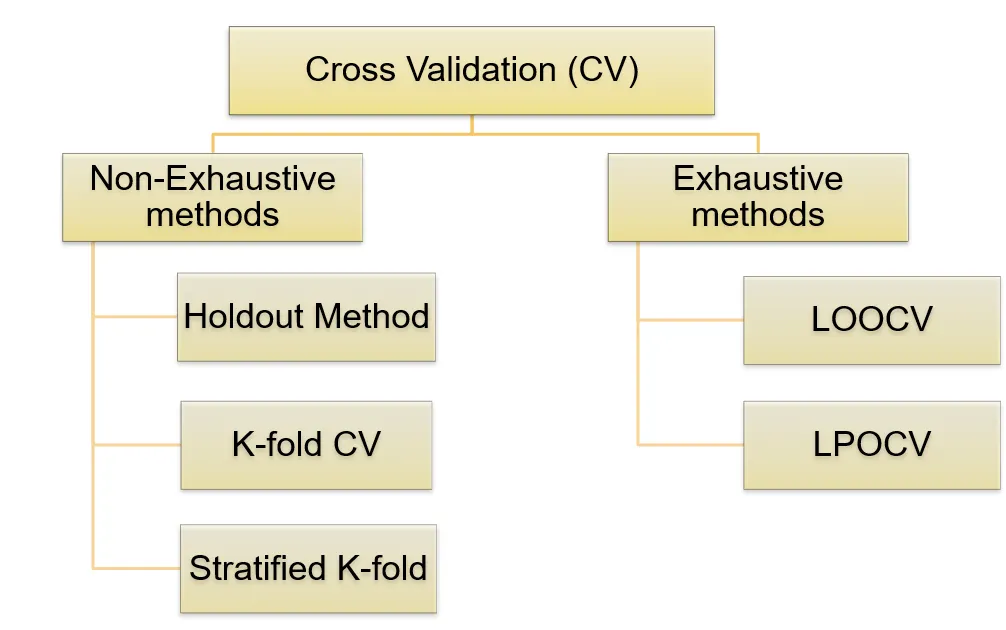
1. Hold-Out Method

• Dataset split into training and testing sets (e.g., 70% train, 30% test).
  
• Simple but can produce biased results depending on the split.

2. K-Fold Cross Validation

• Dataset divided into k folds (e.g., 10).
  
• Model trained on k-1 folds and tested on the remaining one.
  
• Results averaged across folds.
  
• Most popular technique.

3. Stratified K-Fold Cross Validation

• Ensures each fold maintains the same class proportion as the dataset.
  
• Useful for imbalanced datasets (e.g., fraud detection).

4. Leave-One-Out Cross Validation (LOOCV)

• Each data point is treated as a test set once.
  
• Computationally expensive but unbiased.

5. Leave-P-Out Cross Validation

• Similar to LOOCV but leaves out p points at a time.
  
• Provides flexibility but increases complexity.

6. Repeated Random Sub-Sampling

• Randomly splits data multiple times.
  
• Results averaged over repetitions.

7. Time Series Cross Validation

• Designed for sequential data like stock prices or sensor data.
  
• Ensures training is always before testing chronologically.

Real-Time Examples of Cross Validation in Action

• Healthcare: Predicting patient readmission rates using logistic regression validated through stratified K-Fold.
  
• Finance: Credit card fraud detection with imbalanced data handled by stratified sampling.
  
• Retail: Customer churn prediction using repeated k-fold validation.
  
• Sports Analytics: Player performance predictions using LOOCV for small datasets.
  
• Time Series Forecasting: Stock market predictions validated with time series cross validation.
  
• NLP: Sentiment analysis models validated with stratified k-fold to balance class distribution.
  
• Computer Vision: Image classification with CV combined with augmentation strategies.

Cross Validation vs Train-Test Split

Aspect	Train-Test Split	Cross Validation
Bias	Higher	Lower
Variance	Higher	Lower
Computation	Fast	Slower
Reliability	Less robust	More robust

Advantages of Cross Validation

• Provides more reliable estimates of model performance.
  
• Reduces dependency on a single random train-test split.
  
• Helps optimize hyperparameters effectively.
  
• Works for both regression and classification tasks.

Limitations and Challenges of Cross Validation

• Computationally expensive for large datasets.
  
• Time-consuming in deep learning.
  
• Doesn’t work directly with time-dependent data unless modified.
  
• May still suffer from data leakage if preprocessing is not done carefully.

Hyperparameter Tuning with Cross Validation

Cross validation is the backbone of grid search and random search in hyperparameter tuning.

For example:

• Training a Random Forest with different numbers of trees.
  
• Using cross validation to pick the best model based on accuracy/F1-score.

In sklearn, this is done with GridSearchCV or RandomizedSearchCV.

Cross Validation in Sklearn (Python Code Examples)

from sklearn.model_selection import cross_val_score, KFold

from sklearn.linear_model import LogisticRegression

from sklearn.datasets import load_iris

# Load dataset

X, y = load_iris(return_X_y=True)

# Define model

model = LogisticRegression(max_iter=200)

# Define K-Fold cross validation

kfold = KFold(n_splits=10, shuffle=True, random_state=42)

# Evaluate model

results = cross_val_score(model, X, y, cv=kfold)

print("Cross Validation Accuracy: %.3f (%.3f)" % (results.mean(), results.std()))

Computational Considerations

• Time Complexity: CV is costly for large datasets — e.g., k=10 requires 10x training time.
  
• Parallelization: Using libraries like Scikit-learn (n_jobs=-1) or Spark MLlib for distributed CV.
  
• Approximate CV: Subsampling large datasets for quicker evaluation.
  
• GPU vs CPU CV: Tradeoffs when training deep learning models.

Cross Validation in Deep Learning

• Why Rarely Used in DL: Due to high training costs; typically train-validation split is preferred.
  
• Alternatives: Early stopping, Bayesian optimization, or transfer learning.
  
• When Useful: Small datasets where robust evaluation is crucial.

Cross Validation and Hyperparameter Tuning

• Grid Search CV: Exhaustive search across hyperparameter space.
  
• Randomized Search CV: Efficient when hyperparameters are continuous and large.
  
• Bayesian Optimization + CV: Using probabilistic models for tuning while validating via CV.
  
• Nested CV for Fair Comparison: Avoids overfitting when comparing tuned models.

Common Mistakes in Cross Validation

• Data Leakage: Preprocessing (scaling, feature selection) done before splitting.
  
• Improper Shuffling: Time-series data randomly split leading to leakage.
  
• Metric Misinterpretation: Reporting accuracy without context in imbalanced datasets.
  
• Improper Group Handling: Cross-validation without GroupKFold in grouped data leads to overestimation.

Hands-On Example with Scikit-learn

• Regression Example:
  
  • Predict house prices using Boston Housing dataset with k-Fold CV.
    
• Classification Example:
  
  • Use Breast Cancer dataset with stratified k-Fold CV.
    
• Code Snippets: Provide Python examples using cross_val_score, GridSearchCV, and StratifiedKFold.

Visualizations for Better Understanding

• Diagram of k-Fold CV: Showing how data is split into folds.
  
• Nested CV Illustration: Inner vs outer loops for hyperparameter tuning.
  
• Walk-Forward Validation Timeline: Visual explanation for time-series.

Cross Validation vs Train-Test Split

• Train-Test is faster but less reliable.
  
• Cross Validation provides more robust error estimates.
  
• Hybrid approaches: using CV for model selection, then a holdout set for final validation.

Best Practices for Implementing Cross Validation

• Always use stratified folds for classification.
  
• Standardize or normalize data inside the cross validation loop.
  
• Be mindful of time series order when dealing with sequential data.
  
• Combine with hyperparameter tuning for better results.

Industry Use Cases of Cross Validation

1. Healthcare AI – Predicting patient disease progression.
   
2. Banking & Finance – Fraud detection, credit risk modeling.
   
3. Retail & E-commerce – Customer lifetime value prediction.
   
4. Autonomous Vehicles – Object detection validation across scenarios.
   
5. Natural Language Processing (NLP) – Sentiment classification with stratified folds.

Future of Cross Validation in AI/ML

• Automated ML Pipelines: AutoML frameworks integrating CV seamlessly.
  
• Adaptive Cross Validation: Dynamically choosing fold sizes based on data.
  
• Federated Cross Validation: CV in privacy-preserving distributed ML setups.
  
• Hybrid CV with Transfer Learning: Using pre-trained models with limited CV.

Conclusion

Cross validation is more than just a validation technique—it’s the gold standard for evaluating machine learning models. Whether you’re tuning hyperparameters, comparing models, or working with imbalanced datasets, cross validation ensures your model can generalize to real-world data.

By adopting the right type of cross validation for your data and problem type, you not only improve model accuracy but also build trust in your predictions.

If you’re working with machine learning, mastering cross validation is non-negotiable.

FAQ’s