When evaluating the performance of a machine learning classification model, the Confusion Matrix is one of the most powerful tools for visualizing predictions. But when combined with Jacobian matrices, it becomes a strong analytical framework for understanding model sensitivity, optimization, and feature influence.
In this guide, we will break down how the Confusion Matrix Jacobian works, why it matters, and how you can use it to make smarter decisions in machine learning projects.
Why Confusion Matrix is Essential in Machine Learning
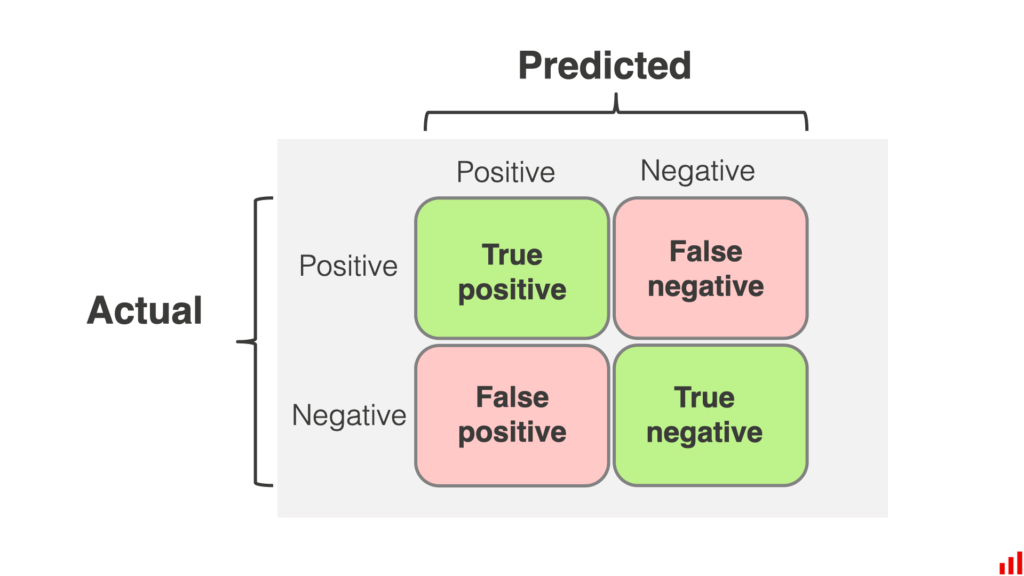
A confusion matrix provides a detailed breakdown of True Positives (TP), True Negatives (TN), False Positives (FP), and False Negatives (FN), helping us:
- Measure accuracy beyond a single percentage score.
- Identify class imbalance problems.
- Understand the trade-off between precision and recall.
For example:
If your spam email classifier labels 95% of emails as non-spam correctly but fails at detecting 20% of spam emails, this can lead to real-world security issues.
Understanding the Jacobian in Mathematics and ML
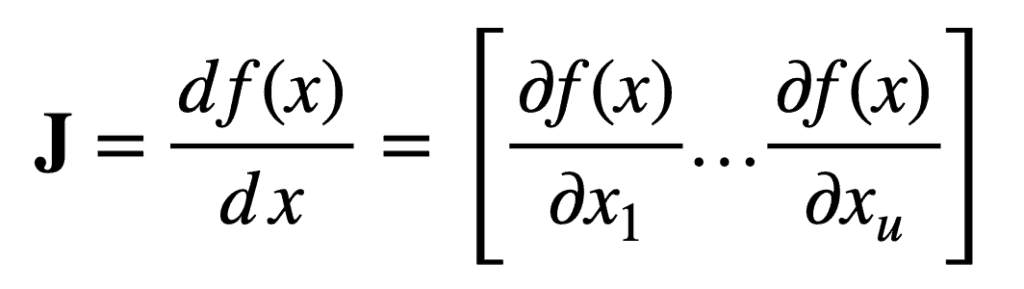
The Jacobian is a matrix of all first-order partial derivatives of a vector-valued function. In machine learning, it is crucial for:
- Measuring sensitivity of model output with respect to input parameters.
- Gradient-based optimization in deep learning.
- Stability analysis in control systems.
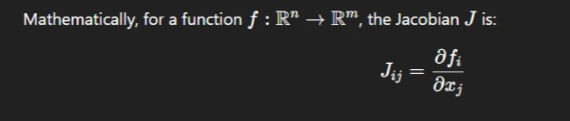
Confusion Matrix Jacobian: Bridging Evaluation and Optimization
When we talk about the Confusion Matrix Jacobian, we refer to calculating the rate of change in confusion matrix values with respect to input parameters or model hyperparameters.
Benefits:
- Optimization: Fine-tuning model thresholds for better F1 scores.
- Sensitivity Analysis: Understanding how changes in feature importance affect classification performance.
Key Components of a Confusion Matrix
| Prediction \ Actual | Positive | Negative |
| Positive | TP | FP |
| Negative | FN | TN |
- True Positives (TP): Correctly predicted positives.
- True Negatives (TN): Correctly predicted negatives.
- False Positives (FP): Incorrectly predicted positives.
- False Negatives (FN): Missed positives.
Mathematical Representation of the Jacobian in Classification Model
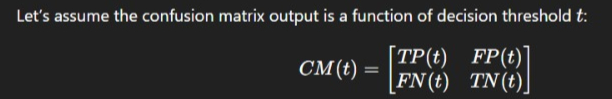
Jacobian with respect to ttt will show how small changes in the threshold affect TP, FP, FN, and TN.
Real-Time Example: Spam Email Classification
Imagine you’re building a spam filter using logistic regression:
- At threshold t=0.5t = 0.5t=0.5, you get TP = 80, FP = 10, FN = 20, TN = 90.
- If you adjust ttt slightly, the confusion matrix changes.
- The Jacobian tells you how sensitive each value is to threshold changes.
This helps you balance recall and precision depending on business needs.
Step-by-Step: Computing the Confusion Matrix Jacobian in Python
import numpy as np
from sklearn.metrics import confusion_matrix
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split# Example dataset
X = np.random.rand(200, 4)
y = np.random.randint(0, 2, 200)# Train model
model = LogisticRegression()
model.fit(X, y)
probs = model.predict_proba(X)[:, 1]# Function to compute confusion matrix at a given threshold
def cm_at_threshold(threshold):
preds = (probs >= threshold).astype(int)
return np.array(confusion_matrix(y, preds))# Numerical approximation of the Jacobian
threshold = 0.5
delta = 0.01
J = (cm_at_threshold(threshold + delta) - cm_at_threshold(threshold - delta)) / (2 * delta)
print("Jacobian of Confusion Matrix:\n", J)Visualizing the Confusion Matrix Jacobian
Definition Link – Combines the confusion matrix (model performance evaluation) with the Jacobian matrix (sensitivity of outputs to parameter changes).
Purpose – Shows how small changes in model parameters affect each cell of the confusion matrix (TP, TN, FP, FN).
Visualization Method – Commonly uses heatmaps to highlight magnitude and direction of change for each metric.
Insights – Helps identify which parameters most influence accuracy, precision, recall, or other classification metrics.
Trade-off Detection – Reveals areas where improving one metric (e.g., recall) may worsen another (e.g., specificity).
Advanced Use – Can integrate dimensionality reduction (PCA, t-SNE) for high-dimensional models and enable interactive exploration for parameter tuning.
Including visual aids helps interpret results:
- Heatmaps to show confusion matrix values.
- Surface plots for Jacobian sensitivity across thresholds.
Common Pitfalls and How to Avoid Them
- Overfitting to metrics: Don’t optimize just for accuracy; consider F1 score.
- Ignoring class imbalance: Always balance datasets before training.
- Misinterpreting Jacobian values: Sensitivity ≠ importance.
Real-World Applications Across Industries
- Healthcare: Detecting disease with optimized sensitivity.
- Finance: Fraud detection models tuned for minimal false negatives.
- Manufacturing: Predictive maintenance with minimal downtime misclassifications.
External Tools and Resources
- Scikit-learn Confusion Matrix Documentation
- NumPy Gradient & Jacobian
- Purpose – External tools and resources supplement in-house capabilities by providing specialized functions, datasets, or visualization options.
- Data Analysis Tools – Platforms like Excel, Tableau, or Power BI help in exploring and presenting results more effectively.
- Machine Learning Libraries – Frameworks such as scikit-learn, TensorFlow, or PyTorch offer pre-built methods for computing confusion matrices and Jacobians.
- Visualization Utilities – Tools like Matplotlib, Seaborn, or Plotly allow creation of detailed and interactive performance plots.
- Learning Platforms – Websites like Analytics Vidhya, Kaggle, or Coursera provide tutorials, datasets, and case studies to deepen understanding.
- laboration Tools – GitHub, Google Colab, and Jupyter Notebooks enable sharing code, experiments, and analysis with peers.
Conclusion and Best Practices
Combining the Confusion Matrix with the Jacobian gives ML practitioners a deeper, sensitivity-aware evaluation tool. This ensures models aren’t just accurate, but also robust and adaptable to real-world changes.



