Applications in data mining and machine learning depend heavily on classification methods. Almost 70% of data science problems are classification problems. Logistic regression is a popular and practical regression technique for resolving the binary classification problem, while there are many other classification problems available. Spam detection is one of the many classification problems that may be solved with logistic regression. Other instances include predicting a consumer’s likelihood of purchasing a specific product, determining whether a customer would churn, determining whether a user will click on an advertisement link, and many more.
One of the simplest and most widely used machine learning techniques for two-class classification is logistic regression. It can serve as the foundation for any binary classification problem and is simple to implement. Deep learning benefits from its fundamental principles as well. The correlation between 1 dependent binary variable and independent variables is described and estimated by logistic regression.
You will learn the definition, operation, and appropriate application of logistic regression in this blog post. We’ll also go over a real-world example and go over the key concepts one by one.
What is Logistic Regression?
A statistical technique called logistic regression uses one or more independent variables to predict the probable outcome of a binary result, such as yes/no, pass/fail, or 0/1. Logistic regression is intended for classification problems with categorical output, as opposed to linear regression, which predicts continuous values.
Example:
To predict will a student pass(1)/fail(0) in an examination? The solution is entirely based on the no.of hours studied is a classic use case for logistic regression.
Logistic Regression Under the Hood
Logistic regression is more than just a black-box model. Understanding what happens internally helps you interpret results, debug models, and improve performance.
Linear Combination of Inputs:
Logistic regression starts with a linear combination of features:
z=β0+β1X1+β2X2+…+βnXn
Sigmoid Transformation:
The linear combination is then passed through a sigmoid function to squash outputs between 0 and 1:
P(Y=1∣X)=1 / 1+e-z
This probability output is the model’s prediction of belonging to the positive class.
Decision Boundary:
Typically, a threshold of 0.5 is used:
P>0.5⇒Y=1
P≤0.5⇒Y=0
How Does Logistic Regression Work?
Initialization: Start with initial guesses for coefficients (β\betaβ)
Forward Pass: Compute predicted probabilities using the sigmoid function
Loss Calculation: Use log loss / binary cross-entropy to measure prediction error:
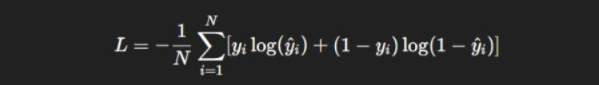
Optimization: Adjust coefficients using gradient descent to minimize the loss
Convergence: Repeat until the loss stops decreasing significantly
Coefficients of Logistic Regression
- Coefficients (βi\beta_iβi) indicate the impact of each independent variable on the log-odds of the outcome:
log-odds=ln(p/1−P)=β0+β1X1+…+βnXn
- Positive coefficient → increases likelihood of Y=1Y=1Y=1
- Negative coefficient → decreases likelihood of Y=1Y=1Y=1
Example Interpretation:
If β1=0.8 for “hours studied”:
- Odds ratio = e0.8≈2.23 → each additional hour studied doubles the odds of passing.
Logistic Regression Equation and Odds
- Logistic regression models log-odds, not probabilities directly:
Odds= p / 1−P=eβ0+β1X1+…+βnXn
- By taking the natural log of odds, we get a linear relationship with features.
- This makes logistic regression both interpretable and powerful for binary classification.
Use Cases of Logistic Regression
| Domain | Example Use Case |
| Healthcare | Disease prediction (e.g., cancer yes/no) |
| Finance | Credit risk assessment (default yes/no) |
| Marketing | Customer conversion prediction |
| Cybersecurity | Detecting fraudulent logins |
| HR | Predicting employee attrition |
| E-commerce | Predicting purchase likelihood |
Logistic regression is ideal when you need probabilities, interpretability, and a simple yet effective model.
How to Evaluate a Logistic Regression Model?
- Confusion Matrix – Shows true positives, true negatives, false positives, false negatives
- Accuracy – Fraction of correct predictions
- Precision & Recall – Important when classes are imbalanced
- F1-Score – Harmonic mean of precision and recall
- ROC Curve & AUC – Measure model’s discrimination ability
Terminologies Involved in Logistic Regression
Dependent Variable (Y): Binary outcome (0/1)
Independent Variable (X): Predictor features
Log-Odds: Natural logarithm of the odds
Odds Ratio: How odds change with a one-unit change in X
Sigmoid Function: Maps linear combination of inputs to probability
Log Loss / Binary Cross-Entropy: Loss function used to optimize the model
Logistic Regression Equation
The logistic regression is obtained from the linear regression equation by applying a sigmoid function to it.
The equation of Linear Regression is,

Where,
y = dependent variable
x = independent variable
β₀,β₁,β₂,βₙ = coefficientsSigmoid Function:
1
P = 𑁋𑁋𑁋𑁋𑁋𑁋
1 + e⁽-y⁾
Applying the Sigmoid function on Linear Regression:
1
P = 𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋𑁋
1 + e-⁽β₀ + β₁X₁ + β₂X₂ +.....+ βₙXₙ⁾=> p / 1 – p
P
ln ( 𑁋𑁋𑁋) = β₀ + β₁X₁ + β₂X₂ +.....+ βₙXₙ1 – P
>>> The above equation is obtained after applying the logarithm.
Types of Logistic Regression

There are 3 forms of logistic regression determined based on the categories:
- Binomial
In binomial logistic regression, only 2 types of dependent variables are possible, like 0/1, pass/fail, true/false, spam/not spam, positive/negative, etc.
- Multinomial
In multinomial logistic regression, 3 or more unordered types of dependent variables are possible, such as “cat”, “dogs”, or “sheep”.
- Ordinal
In ordinal logistic regression, 3 or more ordered types of dependent variables are possible, such as “low”, “medium”, or “high”.
Example: Predicting whether a tumor is cancerous or not cancerous based on its size
Python Code
import numpy as np
from sklearn import linear_model
# Tumor sizes (in centimeters)
X = np.array([3.78, 2.44, 2.09, 0.14, 1.72, 1.65, 4.92, 4.37, 4.96, 4.52, 3.69, 5.88]).reshape(-1, 1)
# Labels: 0 = not cancerous, 1 = cancerous
y = np.array([0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1])
# Create and train the logistic regression model
logr = linear_model.LogisticRegression()
logr.fit(X, y)
# Predict if a tumor of size 3.46 cm is cancerous
prediction = logr.predict(np.array([[3.46]]))
print("Prediction (0 = not cancerous, 1 = cancerous):", prediction[0])
# Predict probability
probability = logr.predict_proba(np.array([[3.46]]))
print("Probability [not cancerous, cancerous]:", probability[0])Output
Prediction (0 = not cancerous, 1 = cancerous): 0
Probability [not cancerous, cancerous]: [0.50241666 0.49758334]Uses of Logistic Regression
- The model coefficients are simple to understand and interpretable.
- Suitable for large data sets, i.e., quick to train.
- It can handle 0/1, true/false, and yes/no predictions with ease (Ideal for Binary Categorization).
- Probabilistic Output – it gives the probability of a class, not just the label.
Applications of Logistic Regression
| Domain | Example Use Case |
| Healthcare | Predicting disease presence or absence |
| Marketing | Customer conversion prediction |
| Finance | Credit risk analysis (default or not) |
| Cybersecurity | Detecting whether a login attempt is fraudulent |
| HR | Predicting Employee Attrition |
Key Properties of the Logistic Regression Equation
Logistic regression is widely used in machine learning for binary classification because of its unique properties. Understanding these properties helps in interpreting the model and applying it effectively.
Non-linearity in Probability Space
- Although the linear combination of features (β0+β1X1+…+βnXn) is linear, the sigmoid function transforms it into a non-linear probability output between 0 and 1.
- This allows logistic regression to handle non-linear relationships in terms of probability, even with a linear decision boundary.
Output Range Between 0 and 1
- Logistic regression outputs probabilities P(Y=1∣X) strictly in the range (0,1).
- This property ensures that predictions are interpretable as probabilities, which is ideal for classification tasks.
Interpretability of Coefficients
- Coefficients (βi) can be interpreted in terms of log-odds:
log-odds=ln(p / 1−P)=β0+β1X1+…+βnXn - Exponentiating a coefficient gives the odds ratio, showing the effect of a one-unit change in the feature on the odds of the outcome.
S-Shaped (Sigmoid) Curve
- The logistic function produces an S-shaped curve, which models gradual transitions from 0 to 1.
- This smooth transition is useful for predicting probabilities and making threshold-based decisions.
Monotonicity
- The probability increases monotonically with the linear predictor.
- Higher values of the linear combination correspond to higher probabilities of the positive class.
Linearity in Log-Odds
- While the output probability is non-linear, the log-odds are linear in the predictors.
- This linearity makes it easy to understand the relationship between features and the outcome.
Probabilistic Interpretation
- Logistic regression provides direct probability estimates rather than just categorical labels.
- For example, a predicted probability of 0.8 indicates an 80% likelihood of the positive class.
Threshold-Based Classification
- By default, logistic regression classifies outcomes using a 0.5 probability threshold, but this threshold can be adjusted depending on the application (e.g., fraud detection may use a lower threshold).
Robustness to Outliers in X, but Sensitive to Outliers in Log-Odds
- Logistic regression is generally robust to small deviations in feature values.
- However, extreme input values can push the linear combination into the saturation region of the sigmoid function, where gradients become very small (related to vanishing gradients).
Assumptions for Logistic Regression:
- The dependent variable must be categorical.
- The independent variable should not have multicollinearity.
- Observations are independent.
- The dependent variable is binary or categorical.
- Features should have minimal multicollinearity.
Conclusion
In machine learning, logistic regression continues to be one of the most used and successful methods, particularly for problems related to binary classification. Its interpretability, adaptability, and mathematical simplicity make it an effective base model for experts and a perfect place to start for newbies.
You can confidently begin using logistic regression in your data projects if you understand how it operates, from the sigmoid function to practical applications!
Durgesh Kekare, Author
FAQ’s
What are the three types of logistic regression?
The three types of logistic regression are Binary Logistic Regression (two possible outcomes), Multinomial Logistic Regression (three or more unordered outcomes), and Ordinal Logistic Regression (three or more ordered outcomes).
What is a real life example of logistic regression?
A real-life example of logistic regression is predicting whether a customer will buy a product (yes/no) based on features like age, income, and browsing behavior.
What is the main purpose of using logistic regression?
The main purpose of logistic regression is to predict the probability of a categorical outcome, typically binary, based on one or more predictor variables.
What is the formula for logistic regression?
The formula for logistic regression is:
P(Y=1)=1/1+e−(β0+β1X1+β2X2+…+βnXn)
It calculates the probability that the dependent variable Y equals 1 based on the predictor variables
X1,X2,…,Xn.
Who uses logistic regression?
Logistic regression is used by data scientists, statisticians, and analysts across industries like healthcare, finance, marketing, and social sciences to predict categorical outcomes such as disease presence, customer churn, or loan default.




