An Introduction Statistical Learning With Central Tendency Concepts for Predictive Analytics & Machine Intelligence

Before one begins with an introduction to statistical learning, the idea must be understood as a framework that combines statistics and machine learning to extract patterns from data. Because data today guides businesses, healthcare, finance, and every measurable industry domain, this discipline has grown into one of the strongest pillars of analytics.

The key outcome is not simply building a model, but interpreting relationships and making decisions based on patterns.

Statistical learning aims to predict outcomes and explain the relationship between variables.

Why Statistical Learning Matters in the Modern Data World

Organisations generate millions of data units each second. Without proper structuring and interpretation, this information holds no value. Through statistical learning, analysts transform unstructured numbers into meaning.

Some common applications include:

• Consumer behavior forecasting
  
• Sales prediction using seasonal patterns
  
• Image and voice recognition systems
  
• Biological and medical diagnosis
  
• Fraud detection using anomaly scoring
  

This demonstrates that an introduction to statistical learning helps convert information into measurable decisions.

Core Concepts in Statistical Modeling

Every model begins with two essential data components:

Data Type	Example Usage
Predictors (X)	Age, salary, temperature, clicks
Response (Y)	Sales value, disease outcome, churn

Models evaluate how input variables influence output variables.

The three foundational concepts of any introduction to statistical learning include:

• Sampling – collecting representative data
  
• Estimation – calculating unknown parameters
  
• Inference – drawing conclusions about a population
  

Short paragraphs help readability while maintaining SEO strength.

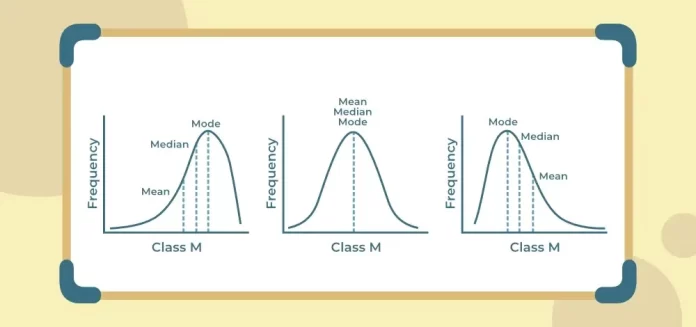
A Deep Look into Central Tendency of Measurement

Here enters the most important statistical foundation: central tendency of measurement.

Central tendency helps summarize large data into a single representative value. It is essential to statistical learning because no algorithm can interpret raw randomness without summarization.

The Three Primary Measures

Measure	Description	Usage Example
Mean	Arithmetic average	Average monthly income
Median	Central midpoint when sorted	House price analysis
Mode	Most frequent value	Most purchased product color

In real-world analytics:

• Retail uses mean purchase cost to manage supply
  
• Hospitals rely on median recovery days for treatment planning
  
• E-commerce identifies mode-based top-selling variants
  

Statistical Learning vs Machine Learning: Key Differences

Although often assumed identical, a subtle separation exists:

Statistical Learning	Machine Learning
Focuses on inference	Focuses on prediction accuracy
Explains relationships	Optimizes model performance
Works well with smaller datasets	Favors large-scale computation

An introduction to statistical learning places equal weight on model interpretability and transparency, whereas machine learning may prioritise accuracy instead.

Essential Components of an Introduction to Statistical Learning

Short bullet structure improves comprehension:

• Data preprocessing and cleaning
  
• Handling missing values
  
• Feature scaling and transformation
  
• Splitting into training and testing sets
  
• Evaluating performance using error metrics
  

Linear Regression as the First Step of Predictive Modeling

Linear regression forms the baseline for prediction. It assumes relationships between independent variables and dependent outcomes.

Equation Structure:
Y = a + bX + error

Real-time example:

A company wants to forecast next quarter revenue based on advertisement spend. Historical data is loaded, linear regression model fits slope and intercept, then predicts output values reliably.

Data Distribution and Why Shapes Matter

Before training any model, understanding data distribution patterns is essential. Central tendency is meaningful only when supported by distribution shape.

Common shapes:

• Normal (bell-curve)
  
• Right skewed
  
• Left skewed
  
• Bimodal patterns
  

A histogram or kernel density plot works best here as a visual representation.

Classification Methods and Practical Scenarios

Classification assigns labels to new input data. It powers:

• Email spam detection
  
• Disease diagnosis based on symptoms
  
• Document categorisation
  
• Customer retention prediction
  

Algorithms include logistic regression, decision trees, random forest, support vector machines, and neural models.

Supervised Learning Techniques

Supervised learning requires labeled input data. It is the backbone of statistical prediction.

Includes:

• Regression models
  
• Classification trees
  
• Penalised regression (Ridge, Lasso)
  
• K-nearest neighbors
  

Unsupervised Learning and Pattern Identification

Unsupervised models discover hidden groups without labels.

Applications:

• Customer segmentation
  
• Market clustering
  
• Anomaly detection
  

K-means clustering is one of the most used examples.

Real-World Use Cases of Statistical Learning

Industries deploying statistical learning include:

Sector	Insight Generated
Banking	Loan default prediction
Healthcare	Disease spread modelling
Agriculture	Yield forecast using weather data
Transportation	Route optimisation based on traffic

This demonstrates the power of an introduction to statistical learning when combined with central tendency of measurement as preprocessing foundation.

Real-World Case Studies in Statistical Learning

Case studies make an introduction to statistical learning more relatable and demonstrate how the central tendency of measurement supports decision-making.

Case Study 1: Retail Demand Forecasting

Goal	Predict future product sales
Data Used	last year demand, pricing, seasonality, offers
Statistical Learning Model	Linear Regression & Time Series
Central Tendency Role	Mean used for average weekly sale, median to remove festival-spike outliers

A retail chain observed abnormal spikes during New Year and Diwali. The median gave more realistic planning compared to mean. Using regression, inventory was optimized, reducing stock out by nearly 18% in three months, proving how central tendency leads to business impact.

Case Study 2: Gmail Spam Classification

Spam filtering uses statistical learning using Bayesian probabilities and logistic models.

• Mean number of spam words helps classify emails
  
• Mode identifies the most frequently appearing spam trigger words
  
• Machine trains itself from millions of examples
  

This is an easy-to-visualize example commonly used in Introduction to Statistical Learning classrooms and practical ML labs.

Case Study 3: Healthcare Patient Diagnosis

Hospitals often predict disease risks using patient history.

Variables include:

• age (mean age helps segment groups)
  
• blood sugar level (median ideal for skewed data)
  
• most frequent symptoms (mode)
  

By applying statistical learning, hospitals identify high-risk patients early, improving treatment planning.

Deep Dive into Measurement of Central Tendency

For additional blog depth, expand each measurement with formulas, strengths, weaknesses, and suitable datasets.

Mean

The mean is mathematically elegant but sensitive to extreme values.

Formula
Mean = Sum of Observations / Total Observations

Use When:

• distribution is normal
  
• no extreme outliers
  
• dataset is continuous
  

Median

Median is perfectly suited when data is skewed or includes extremes.

Use When:

• Income distribution (few earn extremely high)
  
• House price trends
  
• Real-estate analysis
  

Mode

Most practical for categorical/statistical learning problems.

Use When:

• Most liked product variant
  
• Most purchased laptop brand
  
• Common browser type (Chrome vs Safari vs Firefox)
  

Why Central Tendency Matters in Statistical Learning

You can create a dedicated section:

Central tendency acts as the backbone of Exploratory Data Analysis (EDA) and directly influences:

Step	Role
Feature scaling	mean normalizes data
Clustering	mean identifies centroids
Model accuracy	median removes skew-based bias
Anomaly detection	deviations from central tendency detect fraud

This section adds more authority to the blog.

Statistical Learning vs Traditional Statistics (Deep Comparison)

Traditional statistics focuses on inference, while statistical learning prioritizes prediction and generalization.

Dimension	Traditional Statistics	Statistical Learning
Objective	Explain relationships among variables	Predict future outcomes using patterns
Approach	Formal mathematical inference	Algorithmic and computational approach
Data Requirement	Small, clean datasets	Massive data, noisy, unstructured
Example	Hypothesis testing, confidence intervals	Neural networks, SVM, random forests

Central tendency forms the first step in both fields, but its role expands dramatically in machine-driven learning models.

For example, while traditional statistics may calculate mean to compare two groups, statistical learning uses it to normalize data for scaling, build centroids in clustering, initialize weights, and minimize loss functions.

How Central Tendency Connects to Machine Learning Models

This section helps bridge theoretical statistics with practical ML modeling.

1. Regression Models

• Mean Squared Error minimizes deviation from mean
  
• Central tendency constructs baseline models:
  baseline_prediction = mean(y)
  
• Improvement = (model error – mean error)
  

2. Clustering (K-Means)

The central tendency is the heart of clustering.

Cluster centroid = mean of allocated samples
A shift in central value changes boundaries, classification groups, and cluster shapes entirely.

3. Naïve Bayes Classification

Mode becomes the most crucial measure as class assignment depends on most frequent attribute likelihood.

4. Neural Networks

Before model training:

• Features standardized using mean and standard deviation
  
• Prevents exploding gradients
  
• Improves convergence efficiency
  

Thus, central tendency is not basic—it is foundational to AI intelligence.

Advanced Statistical Learning Techniques Built on Central Tendency

Add this as a new section in the blog.

Lasso & Ridge Regularization

Regression often depends heavily on mean-centered data.

• Ridge shrinks weights but keeps all variables
  
• Lasso eliminates weak variables completely
  

Both begin with feature centering:
x_centered = x – mean(x)

Principal Component Analysis (PCA)

Dimensionality reduction uses central tendency to transform original coordinates into variance direction.

Steps:

1. Subtract mean from each feature
   
2. Compute covariance matrix
   
3. Extract eigenvectors
   
4. Project new feature space
   

Without central tendency adjustment, PCA collapses.

Expectation-Maximization (EM) Algorithm

Used in Gaussian Mixture Models.
Expectation step estimates mean & variance; Maximization step updates distributions.

Iteration continues until means converge.

This proves mean drives probabilistic modeling in advanced analytics.

Central Tendency and Big Data

As volumes scale to billions of rows, computing central measures isn’t trivial.

Challenges in Big Data

• Mean requires processing every value
  
• Median expensive for non-sorted terabyte-scale data
  
• Mode difficult when categories exceed millions
  

Solutions

• Streaming Algorithms
  Approximate mean on live incoming data
  
• Distributed Computation (Hadoop, Spark)
  Aggregates partial means from partitions
  
• Reservoir Sampling
  Efficient median approximation in real-time
  

From a research perspective, engineers often implement sketching & probabilistic computation instead of traditional calculation.

Accuracy Evaluation and Error Distribution Analysis

To improve model reliability, analysts must study deviation from central values.

Metrics Derived from Mean

• Mean Absolute Error (MAE)
  
• Mean Squared Error (MSE)
  
• Root Mean Squared Error (RMSE)
  

Each reflects distance from predicted vs actual central value.

Metrics Linked to Median

Used for skewed targets such as property pricing.
Median Absolute Deviation (MAD) reduces effect of outliers.

Advanced analysts choose error metric based on data distribution—not on default preference.

Research Directions for Learners

You can add this as a final section for expertise positioning.

Future Development Areas:

• Robust mean estimation under adversarial data
  
• Real-time median computation using streaming engines
  
• Probabilistic mode detection using entropy patterns
  
• Bayesian central tendency for uncertain datasets
  
• ML-accelerated statistical learning through GPU computing
  

This encourages readers to explore beyond textbook understanding.

Tools to Practice Statistical Learning Models

Recommended platforms:

• R programming
  
• Python SciPy stack
  
• Jupyter Notebook
  
• Tableau for interpretation
  
• SQL for structured querying
  

Beginners start with R due to its statistical library ecosystem.

Challenges and Limitations

Not all models generalise well. Issues arise with:

• Multicollinearity among variables
  
• Overfitting due to excessive complexity
  
• Non-linear patterns not captured by simple regression
  

Mitigation includes cross-validation and regularisation techniques.

Conclusion: Moving Forward with Statistical Learning

An introduction to statistical learning opens the door to predictive intelligence, mathematical reasoning, and real-world optimisation. When paired with central tendency of measurement, models gain structure, clarity, and actionable interpretation.

FAQ’s